 Bisher war die Optimierung im Bezug auf Risiko und Rendite auf zwei Aktien begrenzt. In der Praxis kommen wir mit zwei Werten nicht wirklich weiter.
Bisher war die Optimierung im Bezug auf Risiko und Rendite auf zwei Aktien begrenzt. In der Praxis kommen wir mit zwei Werten nicht wirklich weiter.
In diesem Artikel werden wir mittels OpenOffice Calc und den integrierten Matrix-Funktionen die Berechnung auf eine erweiterte Anzahl von Titeln erhöhen. Im konkreten Beispiel arbeiten wir mit fünf Aktien, aber mit der gleichen Vorgehensweise können wir beliebig viele Wertpapiere einbeziehen.
Die Handlungsanweisungen und Funktionen lassen sich in dieser Form auch in Excel umsetzen.
Dazu erstellen wir eine neue OpenOffice-Datei mit dem Namen „Portfolio_5_Aktien.ods“. Die Kursdaten und Renditeberechnungen kopieren wir aus der zuvor erstellten Datei „Risiko_Rendite.ods“ und fügen sie in das aktuelle Projekt ein.
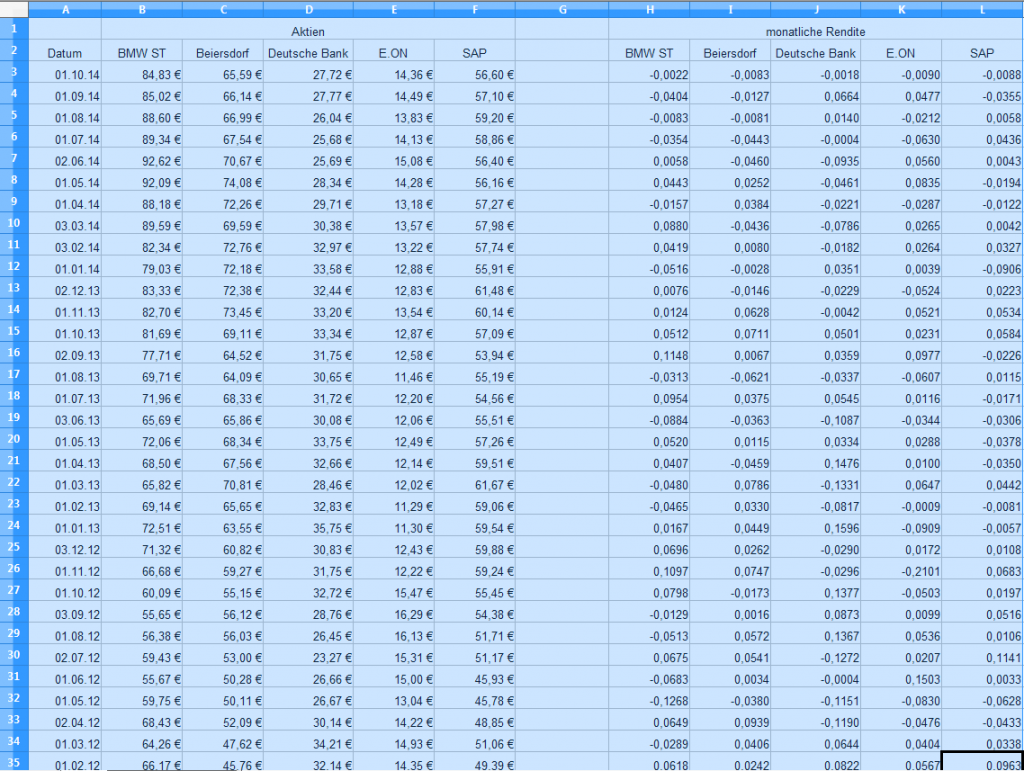 Zur besseren Nachvollziehbarkeit geben wir dem Tabellenblatt den Namen „Daten“. Nun wenden wir uns der zweiten Tabelle zu und vergeben den Namen „Berechnung“ (mit rechter Maustaste auf den Reiter klicken, „Tabelle umbenennen“ wählen und neuen Namen eingeben).
Zur besseren Nachvollziehbarkeit geben wir dem Tabellenblatt den Namen „Daten“. Nun wenden wir uns der zweiten Tabelle zu und vergeben den Namen „Berechnung“ (mit rechter Maustaste auf den Reiter klicken, „Tabelle umbenennen“ wählen und neuen Namen eingeben).
 Um Schreibarbeit zu vermeiden, werden wir eine Funktion anwenden, die wir auch im weiteren Verlauf einsetzen werden: das Transponieren.
Um Schreibarbeit zu vermeiden, werden wir eine Funktion anwenden, die wir auch im weiteren Verlauf einsetzen werden: das Transponieren.
Wie bereits im Artikel „Ein kurzer Ausflug in die Matrix-Algebra“ beschrieben, werden durch das Transponieren die Zeilen und Spalten einer Matrix vertauscht.Klingt kompliziert, ist aber mit einem Tabellenkalkulationsprogramm einfach umzusetzen:
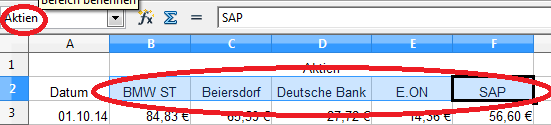
Dazu gehen wir wieder zur ersten Tabelle („Daten“), markieren die Zellen B2 bis F2 mit den Namen der Aktien und vergeben im oberen, linken Feld, das den Zellbereich angibt, den Namen „Aktien“.
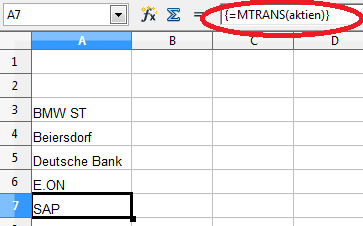
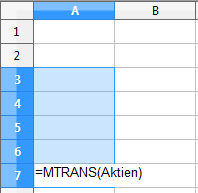
 Wir wechseln zur Tabelle „Berechnung“ und markieren die Zellen A3 bis A7. Die Funktion zum Transponieren lautet „MTRANS“. Entsprechend müssen wir „=MTRANS(Aktien)“ eingeben.
Wir wechseln zur Tabelle „Berechnung“ und markieren die Zellen A3 bis A7. Die Funktion zum Transponieren lautet „MTRANS“. Entsprechend müssen wir „=MTRANS(Aktien)“ eingeben.
Damit das Programm erkennt, dass es sich um eine Matrix-Formel handelt, muss die Eingabe mit „<Strg>+<Shift>+<ENTER>“ abgeschlossen werden.
Anhand der geschweiften Klammer um die Formel, läßt sich erkennen, dass die Formel als Matrix verabeitet wird.
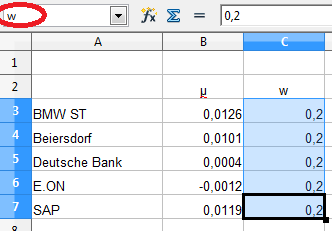
 Im nächsten Schritt vergeben wir die Überschriften. In Spalte B wollen wir die erwarteten Renditen ausgeben, die häufig mit dem griechischen Buchstaben „μ“ (sprich: mü) angegeben werden. Diese Bezeichnung wollen wir an dieser Stelle ebenfalls verwenden (über „Einfügen“ – „Sonderzeichen“).
Im nächsten Schritt vergeben wir die Überschriften. In Spalte B wollen wir die erwarteten Renditen ausgeben, die häufig mit dem griechischen Buchstaben „μ“ (sprich: mü) angegeben werden. Diese Bezeichnung wollen wir an dieser Stelle ebenfalls verwenden (über „Einfügen“ – „Sonderzeichen“).
In Spalte C geben wir die Gewichtung der einzelnen Positionen an. Hierzu verwenden wir die Bezeichnung „w“.
Die zu erwartende Rendite für jede der Aktien haben wir bereits in der Tabelle „Daten“ errechnet. Wir werden die Werte an dieser Stelle wieder über die Funktion „Transponieren“ einlesen.
Dazu wechseln wir wieder zur Tabelle „Daten“, markieren die Renditen in den Zellen H52 bis L52 und vergeben den Namen „E_Rendite“.
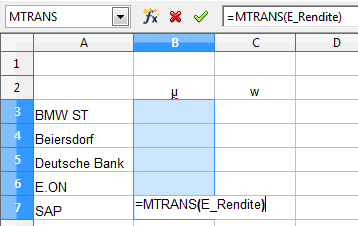
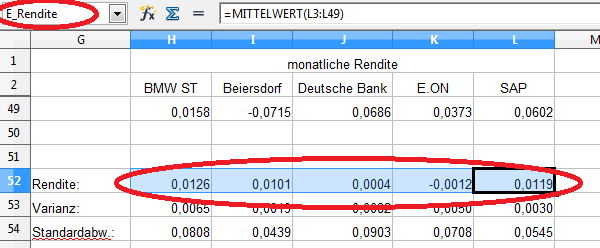 In der Tabelle „Berechnung“ markieren wir die Zellen B3 bis B7, geben die bekannte Formel „=MTRANS(E_Rendite)“ ein und beenden die Eingabe mit „<Strg>+<Shift>+<ENTER>“.
In der Tabelle „Berechnung“ markieren wir die Zellen B3 bis B7, geben die bekannte Formel „=MTRANS(E_Rendite)“ ein und beenden die Eingabe mit „<Strg>+<Shift>+<ENTER>“.
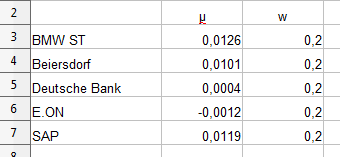
 Für die Gewichtung vergeben wir für alle Aktien den Wert 0,2, d.h. jede Aktie soll einen Anteil am Portfolio von 20% haben. Gerne können Sie auch die Ausgabe in Prozent formatieren, so dass in jedem Feld der Wert 20% erscheint. Für die Berechnung ist dies unerheblich, da 0,2 und 20% vom reinen Zahlenwert identisch sind.
Für die Gewichtung vergeben wir für alle Aktien den Wert 0,2, d.h. jede Aktie soll einen Anteil am Portfolio von 20% haben. Gerne können Sie auch die Ausgabe in Prozent formatieren, so dass in jedem Feld der Wert 20% erscheint. Für die Berechnung ist dies unerheblich, da 0,2 und 20% vom reinen Zahlenwert identisch sind.
 Danach vergeben wir unterhalb die Bezeichnungen für die Berechnungen des Gesamtportfolios.
Danach vergeben wir unterhalb die Bezeichnungen für die Berechnungen des Gesamtportfolios.
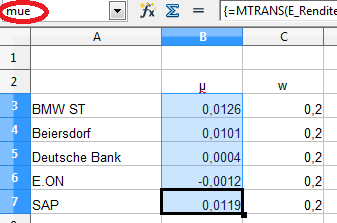
 Zur Berechnung der erwarteten Rendite werden wieder Namen für Zellbereiche eingegeben. Zum einen werden die fünf Einzelrenditen mit „mue“, zum anderen die Gewichtungen der Aktien mit „w“ bezeichnet.
Zur Berechnung der erwarteten Rendite werden wieder Namen für Zellbereiche eingegeben. Zum einen werden die fünf Einzelrenditen mit „mue“, zum anderen die Gewichtungen der Aktien mit „w“ bezeichnet.
Berechnung der Portfolio-Rendite
Schauen wir uns beide Matrizen an, stellen wir fest, dass es sich beidesmal um eine 5×1-Matrix handelt. In unserem Ausflug in die Matrix-Algebra hatten wir aber festgestellt, dass eine 5×1-Matrix nicht mit einer 5×1-Matrix multipliziert werden kann (5x1 * 5x1 => die beiden rot dargestellten Zahlen sind ungleich, daraus folgt, dass keine Matrix-Multiplikation möglich ist).
Sehr wohl kann aber eine 5×1-Matrix mit einer 1×5-Matrix multipliziert werden (1×5 * 5×1 => die beiden grün dargestellten Zahlen sind gleich, daraus folgt, dass die Matrix-Multiplikation möglich ist).
Wie aus einer 5×1-Matrix eine 1×5-Matrix wird, ist uns in der Zwischenzeit bekannt: durch Transponieren der Matrix mittels der Funktion „MTRANS“.
Somit lautet die Formel für die erwartete Portfolio-Rendite:
E(rp) = wT * μ wT steht für w transponiert
In OpenOffice Calc lautet die Funktion für die Matrix-Multiplikation „MMULT“. Somit sieht die komplette Formel wie folgt aus:
=MMULT(MTRANS(w); mue)
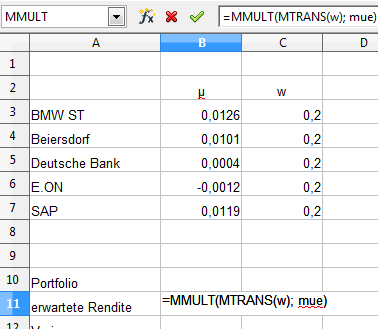 Wir erhalten einen Wert von 0,0068 (auf 4 Nachkommastellen formatiert) oder 0,68% erwartete, monatliche Rendite.
Wir erhalten einen Wert von 0,0068 (auf 4 Nachkommastellen formatiert) oder 0,68% erwartete, monatliche Rendite.
Berechnung der Portfolio-Varianz
Die Formel zur Berechnung der Portfolio-Varianz lautet:
Die Gewichtung „w“ – auch in transponierter Form – ist bekannt.
Neu dadegen ist „S“, die Varianz-Kovarianz-Matrix. Sie wird wie folgt berechnet:
Dabei bezieht sich „A“ auf die periodischen Renditen bezogen auf die mittlere Rendite.
Bei BMW beispielsweise beträgt die erwartete Rendite (mittlere Rendite) über den Beobachtungszeitraum 1,26%. Beträgt die Rendite für eine Periode 2,26%, so wäre der Wert bezogen auf die mittlere Rendite 1 % (2,26% – 1,26%). Liegt die periodische Rendite unter der mittleren Rendite, ist der Wert negativ. Wäre die Rendite einer Periode 0,26%, ergibt sich ein Wert von -1% (0,26% – 1,26%).
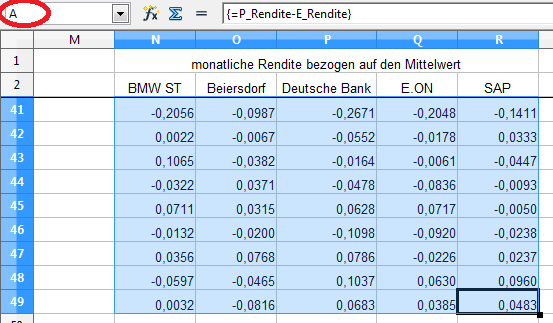
Zur Umsetzung kopieren wir die Überschriften der Zellen H bis L , fügen sie im Bereich N bis R ein und ändern den Text der zellübergreifenden Überschrift auf „monatliche Rendite bezogen auf den Mittelwert“.
 Danach markieren wir alle Datenzellen der monatlichen Renditen von H3 bis L49 und vergeben für den Bereich den Namen „P_Rendite“ (periodische Renditen).
Danach markieren wir alle Datenzellen der monatlichen Renditen von H3 bis L49 und vergeben für den Bereich den Namen „P_Rendite“ (periodische Renditen).
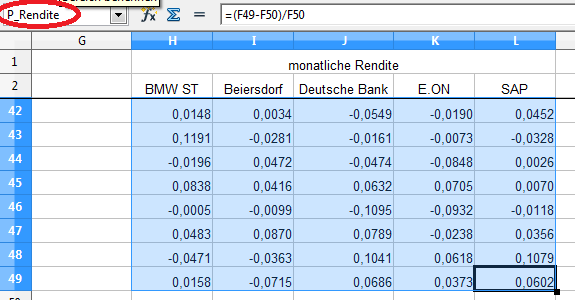 Zur Berechnung der Renditen bezogen auf den Mittelwert setzen wir wieder die Matrix-Algebra ein. Dazu markieren wir die Zellen N3:R49 und subtrahieren von den periodischen Renditen (P_Rendite) die erwartete (mittlere) Rendite, die wir bereits zuvor mit „E_Rendite“ bezeichnet haben.
Zur Berechnung der Renditen bezogen auf den Mittelwert setzen wir wieder die Matrix-Algebra ein. Dazu markieren wir die Zellen N3:R49 und subtrahieren von den periodischen Renditen (P_Rendite) die erwartete (mittlere) Rendite, die wir bereits zuvor mit „E_Rendite“ bezeichnet haben.
 Somit lautet die Formel für unsere Berechnung:
Somit lautet die Formel für unsere Berechnung:
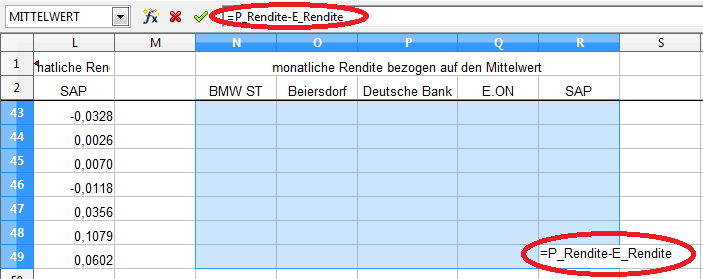 Da es sich um eine Matrix-Berechnung handelt, muss die Formel mit „<Strg>+<Shift>+<ENTER>“ abgeschlossen werden.
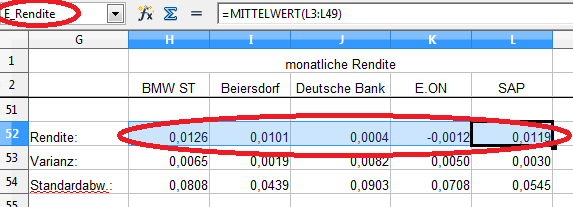
Da es sich um eine Matrix-Berechnung handelt, muss die Formel mit „<Strg>+<Shift>+<ENTER>“ abgeschlossen werden.
Anschließend vergeben wir für den gesamten Bereich den Namen „A“.
 Werfen wir noch einmal einen Blick auf die Formel der Varianz-Kovarianz-Matrix S:
Werfen wir noch einmal einen Blick auf die Formel der Varianz-Kovarianz-Matrix S:
Es ist nur noch „M – 1“ offen. „M“ ist die Anzahl der beobachteten periodischen Renditen, in unserem Fall 47 (H3:H49). Somit ergibt M – 1 = 46.
Diesen Wert tragen wir in unsere Tabelle „Berechnungen“ ein und vergeben für die Zelle F1 den Namen „Perioden“.
 Nun sind wir in der Lage die Varianz-Kovarianz-Matrix S zu erstellen.
Nun sind wir in der Lage die Varianz-Kovarianz-Matrix S zu erstellen.
Wir kopieren die Bezeichnungen der Aktien in Spalte A und fügen sie in Spalte G ein.
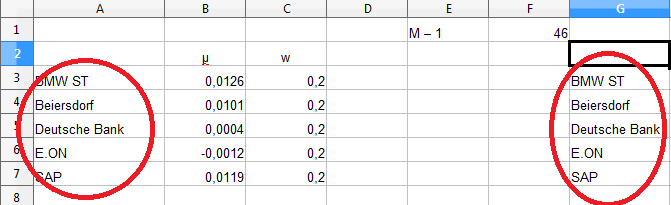 Nun müssen die Bezeichnungen noch in Zeile 2 eingefügt werden.
Nun müssen die Bezeichnungen noch in Zeile 2 eingefügt werden.
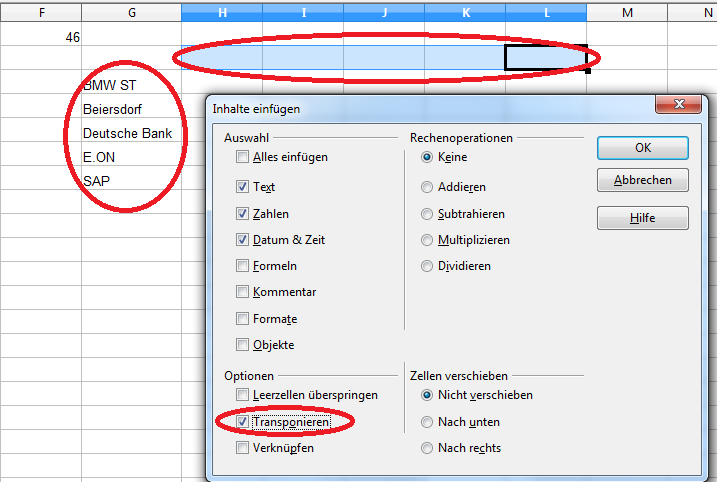
Spalten in Zeilen können wir einfach durch Transponieren einfügen. An dieser Stelle möchte ich eine zweite Möglichkeit zum Transponieren zeigen:
- Kopieren Sie die Zellen G3 bis G7
- Markieren Sie die Zellen H2 bis L2
- Drücken Sie die rechte Maustaste und wählen „Inhalte einfügen“ aus.
Die Aktiennamen werden nun in die Zeile übernommen.
 Jetzt müssen wir die Matrix nach der oben erwähnten Formel mit Inhalten füllen:
Jetzt müssen wir die Matrix nach der oben erwähnten Formel mit Inhalten füllen:
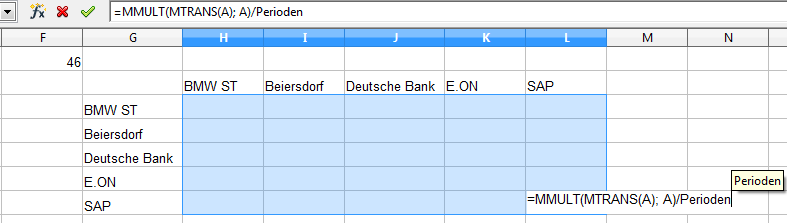 Wir führen eine Matrixmultiplikation mit „A“ transponiert und „A“ durch und teilen das Ergebnis durch die Anzahl der Werte minus 1 (=Perioden). Nach „<Strg>+<Shift>+<ENTER>“ sieht das Ergebnis wie folgt aus:
Wir führen eine Matrixmultiplikation mit „A“ transponiert und „A“ durch und teilen das Ergebnis durch die Anzahl der Werte minus 1 (=Perioden). Nach „<Strg>+<Shift>+<ENTER>“ sieht das Ergebnis wie folgt aus:
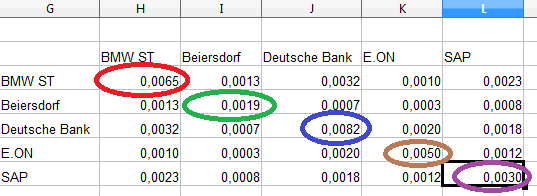 Wir können einfach überprüfen, ob unsere Berechnungen korrekt waren. Die farblich gekennzeichneten Werte müssen den Varianzen entsprechen, die wir in der Tabelle „Daten“ errechnet haben:
Wir können einfach überprüfen, ob unsere Berechnungen korrekt waren. Die farblich gekennzeichneten Werte müssen den Varianzen entsprechen, die wir in der Tabelle „Daten“ errechnet haben:
![]() In diesem Fall stimmen die Ergebnisse überein.
In diesem Fall stimmen die Ergebnisse überein.
Somit stehen wir kurz vor dem Ziel. Wir müssen für die Varianz-Kovarianz-Matrix (H3:L7) noch den Namen „S“ vergeben, ehe wir uns der Varianz des Gesamtportfolios zuwenden können.
Die Formel war:
Im Gegensatz zu einer üblichen Zahlenmultiplikation läßt sich eine Matrix-Multiplikation nicht in der Form A*B*C durchführen. Stattdessen müssen zwei Multiplikationen nacheinander ausgeführt werden:
Die erste Multiplikation innerhalb der Klammer ist „MMULT(MTRANS(w); S)“.
In der zweiten wird obige Multiplikation nochmals mit „w“ multipliziert, wodurch der komplette Ausdruck lautet:
„=MMULT(MMULT(MTRANS(w); S); w)“
Wie immer bei einer Matrix-Funktion muss die Eingabe mit „<Strg>+<Shift>+<ENTER>“ beendet werden.
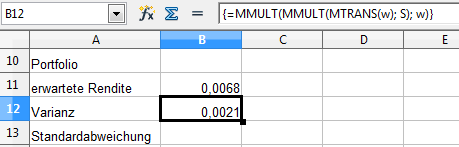 Die Standardabweichung unseres Portfolios ist die Wurzel der Varianz.
Die Standardabweichung unseres Portfolios ist die Wurzel der Varianz.
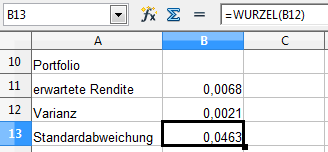 Wir sind nun in der Lage die erwartete Rendite und die Standardabweichung eines Portfolios aus mehr als zwei Aktien zu berechnen.
Wir sind nun in der Lage die erwartete Rendite und die Standardabweichung eines Portfolios aus mehr als zwei Aktien zu berechnen.
Sie können nun ein wenig experimentieren, welche Änderungen sich bei unterschiedlichen Gewichtungen „w“ ergeben.
Im nächsten Artikel werden wir darauf eingehen, wie die Gewichtungen für ein optimales Portfolio mit den vorgegebenen Werten errechnet werden können.


2 Kommentare
Das ist echt der Hammer, danke dafür 😀
Autor
Danke für die Blumen!