Gewichteter gleitender Durchschnitt

Mit dem gewichteten gleitenden Durchschnitt (weighted moving average – WMA) wollen wir einen weiteren Trendfolgeindikator vorstellen.

Ähnlich dem exponentiell gleitenden Durchschnitt werden den aktuelleren Kursen eine höhere Gewichtung zugeordnet.

Nachfolgend wollen wir die Formel für den gewichteten gleitenden Durchschnitt vorstellen.

Wie schon bei den zuvor vorgestellten gleitenden Durchschnitten gilt auch hier, dass Sie die Formel zur praktischen Anwendung in der Regel nicht benötigen, da er in den meisten Charts bei entsprechender Auswahl zur Verfügung steht.

Nur falls Sie eine nicht lineare, flexible Gewichtung vorgeben wollen, sind Sie auf die eigene Berechnung – am einfachsten mittels eines Tabellenkalkulationsprogramm – angewiesen.

Die Formel für den gewichteten gleitenden Durchschnitt lautet:

WMA_t = (c_t * W_n + c_t-1 * W_n-1 + …+ c_t-n+1 * W_n-n+1) / (W₁ + W₂+…+ W_n)

Sie ist weitaus weniger kompliziert, als es auf den ersten Blick ausieht, wie Sie im Beispiel unten sehen werden. Im einzelnen bedeutet:

• WMA_t ist der berechnete gewichtete gleitende Durchschnitt zum aktuellen Zeitpunkt.
• c_t ist der Schlußkurs der verwendeten Periode – meist der Tagesschlußkurs.
• W ist der Gewichtungsfaktor (z.B. “1” am ersten Tag, der in den GD eingeht, “2” am zweiten Tag usw.).
• n entspricht der Dauer über welche der gleitende Durchschnitt berechnet wird (z.B. 10 bei einem 10-Tage-gewichteten gleitenden Durchschnitt).

Zur praktischen Umsetzung wollen wir wieder Wolfgang’s Korbproduktion aus dem Beitrag über den einfachen gleitenden Durchschnitt verwenden:

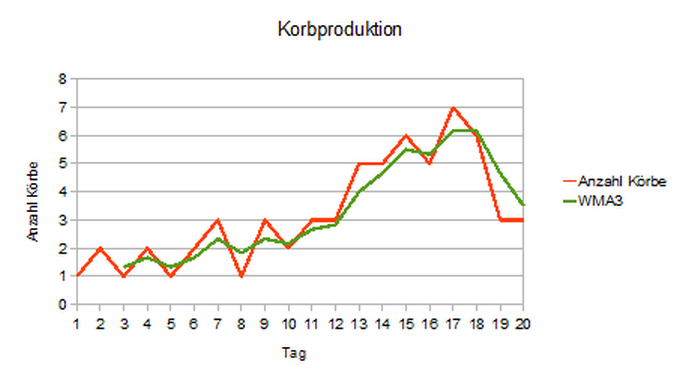
Wir beginnen wieder mit dem 3-Tage-WMA. Den ersten Wert erhalten wir am dritten Tag:

WMA₃ = (c₃ * W₃ + c₂ * W₂ + c₁ * W₁) / (W₁ + W₂+ W₃)

• t = 3, da unser erster Wert nach 3 Tagen berechnet wird.
• => c₃ = 1 (Anzahl Körbe Tag 3), c₂ = 2 (Anzahl Körbe Tag 2), c₁ = 1 (Anzahl Körbe Tag 1)
• n = 3, da wir den 3-Tage WMA einsetzen.
• => W₁ = 1, W₂ = 2, W₃ = 3

WMA₃ = (1 * 3 + 2 * 2 + 1 * 1) / (1 + 2+ 3) = 8 / 6 = 1,33

Am vierten Tag erhalten wir folgenden Wert:

WMA₄ = (c₄ * W₃ + c₃ * W₂ + c₂ * W₁) / (W₁ + W₂+ W₃)

• t = 4, da unser erster Wert nach 4 Tagen berechnet wird.
• => c₄ = 2 (Anzahl Körbe Tag 4), c₃ = 1 (Anzahl Körbe Tag 3), c₂ = 2 (Anzahl Körbe Tag 2)
• n = 3, da wir den 3-Tage WMA einsetzen.
• => W₁ = 1, W₂ = 2, W₃ = 3

WMA₄ = (2 * 3 + 1 * 2 + 2 * 1) / (1 + 2+ 3) = 9 / 6 = 1,50

Usw. bis zu Tag 20 mit folgenden Werten:

WMA₂₀ = (c₂₀ * W₃ + c₁₉ * W₂ + c₁₈ * W₁) / (W₁ + W₂+ W₃)

• t = 20, da unser erster Wert nach 20 Tagen berechnet wird.
• => c₂₀ = 3 (Anzahl Körbe Tag 20), c₁₉ = 3 (Anzahl Körbe Tag 19), c₁₈ = 6 (Anzahl Körbe Tag 18)
• n = 3, da wir den 3-Tage WMA einsetzen.
• => W₁ = 1, W₂ = 2, W₃ = 3

WMA₂₀ = (3 * 3 + 3 * 2 + 6 * 1) / (1 + 2+ 3) = 21 / 6 = 3,50

Wenden wir uns dem 6-Tage WMA zu:

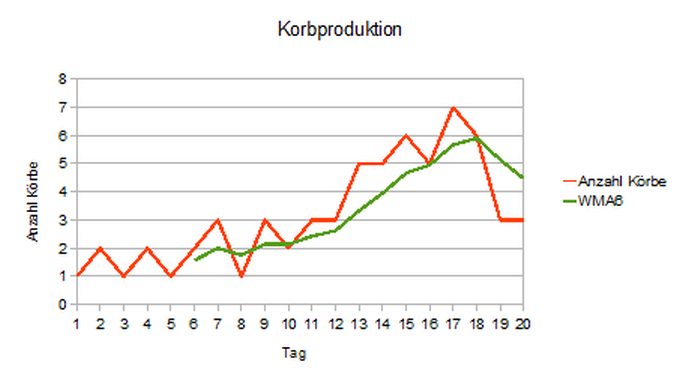Zur Veranschaulichung wollen wir den ersten Wert an Tag 6 berechnen:

WMA₆ = (c₆ * W₆ + c₅ * W₅ + c₄ * W₄ + c₃ * W₃ + c₂ * W₂ + c₁ * W₁) / (W₁ + W₂+ W₃ + W₄ + W₅+ W₆)

• t = 6, da unser erster Wert nach 6 Tagen berechnet wird.
• => c₆ = 2 (Anzahl Körbe Tag 6), c₅ = 1 (Anzahl Körbe Tag 5), c₄ = 2 (Anzahl Körbe Tag 4),
  c₃ = 1 (Anzahl Körbe Tag 3), c₂ = 2 (Anzahl Körbe Tag 2), c₁ = 1 (Anzahl Körbe Tag 1)
  
• n = 6, da wir den 6-Tage WMA einsetzen.
• => W₁ = 1, W₂ = 2, W₃ = 3, W₄ = 4, W₅ = 5, W₃ = 6
  

WMA₆ = (2 * 6 + 1 * 5 + 2 * 4 + 1 * 3 + 2 * 2 + 1 * 1) / (1 + 2+ 3 + 4 + 5 + 6) = 33 / 21 = 1,57

Ansonsten ist noch der bereits bekannte Zusammenhang zu erkennen: je länger der Zeitraum wird, in dem die Werte einer Periode zusammengefasst werden, desto mehr wird die Kurve geglättet.

Zum Abschluß wollen wir noch den 6-Tage-WMA, den 6-Tage-EMA (exponentiell gleitender Durchschnitt) und den 6-Tage-SMA (einfach gleitender Durchschnitt) gegenüberstellen:

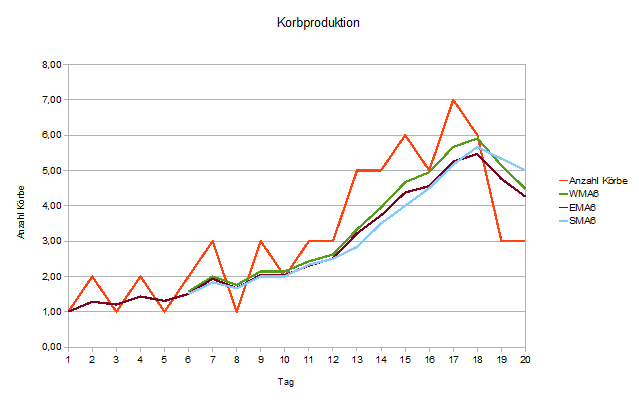Wir erkennen die unterschiedlichen Reaktionszeiten:

Am schnellsten reagiert der gewichtete gleitende Durchschnitt (WMA) vor dem exponentiell gleitenden Durchschnitt. Am trägesten reagiert der einfach gleitende Durchschnitt.

Aber bitte beachten Sie: der Vorteil der schnelleren Reaktionszeit wird mit dem Nachteil der größeren Anfälligkeit gegenüber Fehlsignalen erkauft.

Weitere Beiträge zu dieser Thematik:

• Einfacher gleitender Durchschitt (SMA)
• Exponentiell gleitender Durchschnitt (EMA)