Berechnung des Value at Risk

Die Berechnungen des Value at Risk sind mit den Funktionen der heutigen Tabellenkalkulationsprogrammen relativ einfach umzusetzen.

Neben der Möglichkeit eigene Auswertungen vorzunehmen, verhilft der Einsatz zum besseren Verständnis der Kennzahl.

Im letzten Artikel wurde die Monte Carlo Simulation erwähnt. Obwohl es auch möglich ist, diese Simulation in Excel oder Openoffice zu erstellen, würde es den Rahmen des Artikels sprengen. Sofern Interesse an einer Beschreibung vorliegt, werde ich in einem zukünftigen Artikel gerne dazu eingehen.

Somit verbleiben die historische Simulation und die analytische Methode. Die ersten beiden Schritte sind für beide Methoden gleich, ehe sich die Wege verzweigen. In den folgenden Beispielen wurde Openoffice verwendet. Meines Wissens nach sind die verwendeten Funktionen in Excel identisch.
Bei den Berechnungen wird von einer Wahrscheinlichkeit von 95% und einer Zeitspanne von einem Tag ausgegangen.

Schritt 1: Kursdaten besorgen und einlesen

Kursdaten können in den meisten Finanz- und Börsenportalen als csv-Dateien heruntergeladen werden. Im folgenden Beispiel werden die Daten von Onvista verwendet. Auf anderen Seiten ist die Vorgehensweise ähnlich, nur die jeweilige Zugriffsseite wird sich unterscheiden.

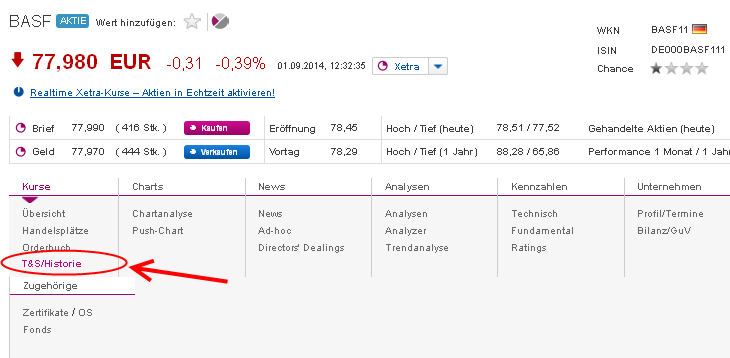Die Aktie von BASF (WPKN: BASF11), die für die Berechnung eingesetzt wird, wurde über das Suchfeld bereits aufgerufen. Nach einem Klick auf “T&S/Historie” öffnet sich eine neue Seite, in deren Mitte sich folgende Daten zeigen:

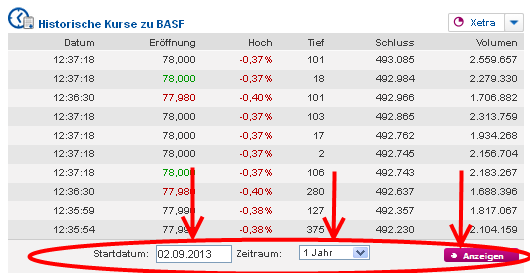Aktuelles Datum war der 01.09.2014. Da die Daten von einem Jahr gewünscht werden, ist als Startdatum logischerweise der 02.09.2013 einzutragen. Nach Betätigen des Buttons “Anzeige” öffnet sich ein separates Fenster mit diversen Daten.

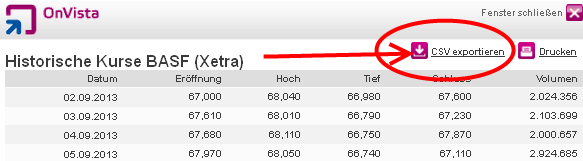
Nun kann die csv-Datei exportiert werden.
Im Tabellenbearbeitungsprogramm können die Daten nun importiert werden, indem die Exportdatei mit der rechten Maustaste bearbeitet und “Öffnen mit” unter Auswahl des Programmes angewählt wird. Alternativ kann das Programm geöffnet und unter “Einfügen / Tabelle aus Datei…” (Openoffice) eingefügt werden.

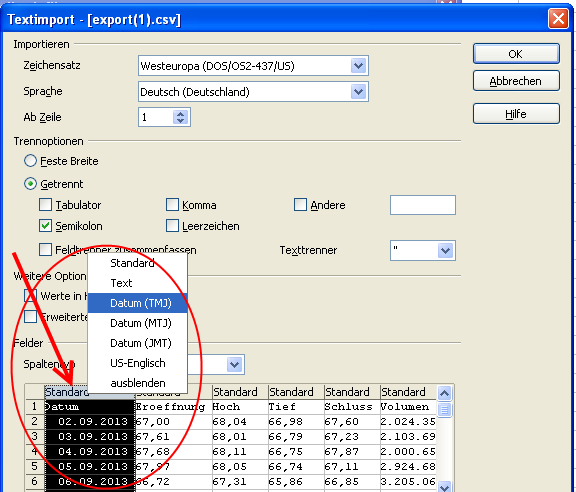Je nach Quelle kann es möglich sein, dass das Datumsfeld als solches deklariert werden muss, um nicht als Textfeld integriert zu werden.

Das Ergebnis sollte dann wie folgt aussehen:

Da für die weitere Auswertung nur die Spalten “Datum” und “Schluss(kurs)” notwendig sind, werden die beiden Spalten in ein neues Arbeitsblatt kopiert (oder die anderen Spalten gelöscht). Anschließend können die Spalten noch etwas in Form gebracht werden, z.B. durch Formatierung des Schlußkurses als Währung.

Schritt 2: Berechnung der täglichen Kursänderungen

Zur Berechnung der täglichen Kursänderungen wird in Spalte C folgende, einfache Formel verwendet: (“Formel am 3.05.2018 revidiert”)

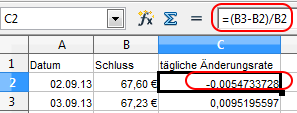Es ist die Differenz zwischen aktuellem und Vortageskurs dividiert durch den Vortageskurs. Diese Berechnung wird bis zum vorletzten Kurswert durchgezogen. Der Wert 0,00547 entspricht entspricht einer Kursänderung von 0,547% bezogen auf den Vortag.

Schritt 3: Berechnung des Value at Risk (historische Simulation)

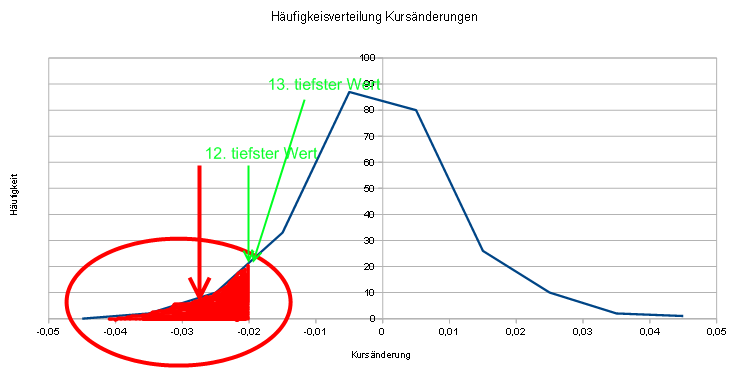
Zum besseren Verständis über die Vorgehensweise bei der Berechnung mittels der historischen Simulation, wurde die Häufigkeit der Kursänderungen in einer Grafik dargestellt:

Zur Erklärung:

Es werden 252 Kurswerte verwendet. 5% der 252 Kurswerte entsprichen 12,6 Werten. Die tiefsten 5% der Werte beginnen folglich zwischen dem 13. tiefsten und dem 12. tiefsten Wert. Also bei ungefähr -0,02 oder -2%. Der Value at Risk wäre demnach bei einem Konfidenzniveau von 95% bei -2%.

Zur Berechnung einer Wahrscheinlichkeit von 99% müssen folglich die niedrigsten 1% der 252 Werte gesucht werden. Das wären 2,52 Werte, womit der Value at Risk zwischen dem 3. tiefsten und dem 2. tiefsten Wert liegt.

Über die Funktion “KKLEINSTE” wird aus den Kursänderungsdaten der 13. kleinste Wert ermittelt, dasselbe wird mit dem 12. kleinsten Wert ausgeführt.

Der 12,6-kleinste Wert wird interpoliert:

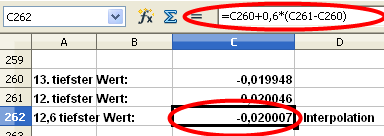Und liefert gleichzeitig unser Ergebnis, den Value at Risk für einen Tag bei 95-prozentiger Wahrscheinlichkeit.

Sinnvoll ist die Umrechnung in einen Prozentwert (* 100% oder Formatierung der Zelle als Prozentzahl).
Bei Bedarf kann der Wert zuletzt noch als absoluter Betrag angegeben werden:

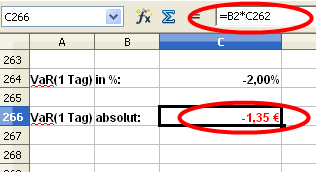Dazu wird der aktuellste Kurs mit dem VaR multipliziert.

Schritt 3: Berechnung des Value at Risk (analytische Methode)

Im Gegensatz zur historischen Simulation, in der die tatsächliche Datenverteilung verwendet wird, wird bei der analytischen Methode die Standardnormalverteilung eingesetzt.

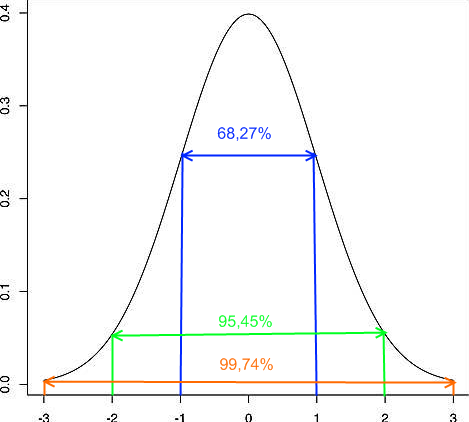Bei der Standardnormalverteilung ist der Mittelwert mit “0” (also symmetrisch zum Nullpunkt) definiert. Die Werte in der x-Achse entsprechen den Vielfachen der Standardabweichung σ.
Es gilt:

zwischen -σ und +σ befinden sich 68,27% aller Werte
zwischen -2*σ und +2*σ befinden sich 95,45% aller Werte
zwischen -3*σ und +3*σ befinden sich 99,74% aller Werte

Soll festgestellt werden, wieviele Werte links der 2-fachen Standardabweichung (-2*σ) liegen, muss einfach von den gesamten 100% der Wert innerhalb +- der 2-fachen Standardabweichung (95,45%) abgezogen und durch zwei geteilt werden (da jeweils links und rechts ein Rand bleibt).

Nach diesem Prinzip könnte über eine Tabelle der Normalverteilung der Wert für 90% gesucht und abgelesen, bei welchem Wert die Kurve geschnitten wird, um den Value at Risko zu ermitteln.
Zu beachten ist noch, dass bei der obigen Verteilung der Mittelwert bei “0” liegt. In der Praxis wird die sogenannte Gaußsche Glocke immer mehr oder weniger zum Nullpunkt hin verschoben sein (d.h. der Mittelwert ≠ 0).

Mit einem Tabellenkalkulationsprogramm sind wir nicht angewiesen, die Werte aus einer Grafik auszulesen, sondern können den Value at Risk direkt berechnen.

Dazu berechnen wir zuerst den Mittelwert (= Außermittigkeit der Glocke).

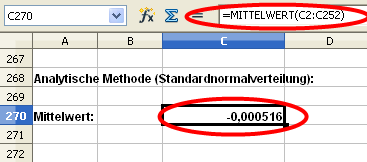Sowie die Standardabweichung σ.

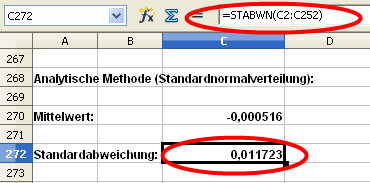Mit der Funktion NORMINV berechnen wir den Schwellwert (mathematische Bezeichnung: Quantil), ab dem die Werte kleiner als das vorgegeben Maß sind.

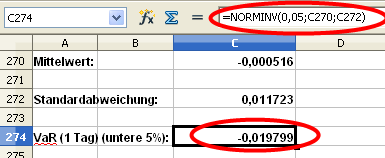Der Wert von 0,05 entspricht 5%, d.h. es wird der Schwellwert gesucht, ab dem 5% der Werte kleiner als der Schwellwert ist. Das entspricht dem Value at Risk bei einer 95% Wahrscheinlichkeit.
Ferner benötigt die Funktion den Mittelwert und die Standardabweichung.

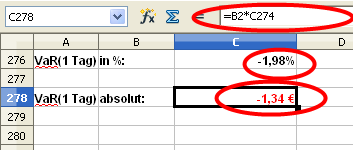Analog zur historische Simulation können zum Abschluß der prozentuale Wert und der Betrag ausgegeben werden.

Mit -1,98% (bzw. -1,34 €) liegt der Value at Risk bei der analytischen Methode in derselben Größenordnung wie in der historischen Simulation mit -2,00% (bzw. -1,35 €).