Nachdem wir zuletzt die Rendite, Varianz, Standardabweichung und Korrelation verschiedener Wertpapiere berechnet haben, wollen wir in diesem Artikel “Risiko-Rendite”-Diagramme erstellen.
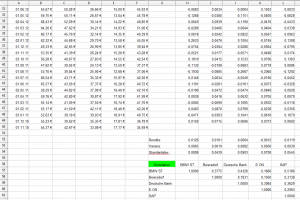
Als Grundlage verwenden wir wieder die OpenOffice Calc-Datei “Risiko_Rendite.ods”, die im Artikel “Korrelation mit OpenOffice Calc berechnen” erstellt wurde.
Das Risiko-Rendite-Diagramm wird mit zwei Aktienpaaren erstellt. Wir wollen mit der Paarung BMW ST – SAP beginnen, die die höchste Korrelation aufweist. Anschließend wollen wir uns Beiersdorf – E.On zuwenden. Dieses Paar weist die geringste Korrelation auf.
Zuerst vergeben wir Überschriften für zwei Spalten. In der ersten Spalte werden die Gewichtungen für die BMW-Aktie, in der zweiten Spalte die Gewichtungen für die SAP-Aktie eingetragen.
Unterhalb der Bezeichnungen werden beide Spalten zur besseren Übersichtlichkeit als Prozentangaben mit zwei Nachkommastellen formatiert.
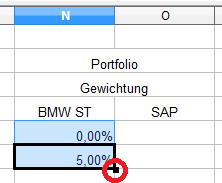
Wir setzen für die Gewichtung 5%-Schritte ein, d.h. der erste Wert der BMW-Aktie ist 0,00%, der zweite Wert 5,00%. Nun markieren wir beide Zellen, gehen mit der Maus auf das kleine, schwarze Quadrat (der Mauszeiger verwandelt sich dabei in ein “+”) und ziehen die Maus bei gedrückter linker Maustaste nach unten bis 100% erreicht werden.
Bei der SAP-Aktie starten wir mit 100%, da die Summe beider Anteile im Portfolio 100% sein muss. Der zweite Wert ist 95%. Danach können wir wieder beide Werte markieren und über das schwarze Quadrat die Wert bis 0% übernehmen. Diese Vorgehensweise läßt auch ohne große Schreibarbeit kleinere Schritte, z.B. im 1%-Bereich zu.
Das Ergebnis sieht nun wie folgt aus:
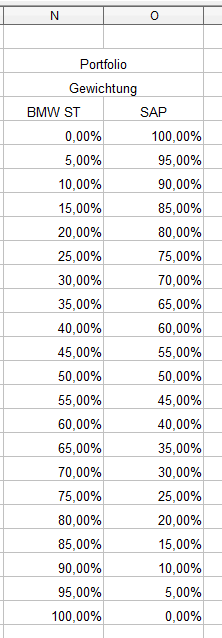Zur Erstellung des Risiko-Rendite-Diagramms sind zwei weitere Spalten erforderlich. Sinnigerweise das Risiko in Form der Standardabweichung und die Rendite in Form des Mittelwertes der periodischen Renditen.
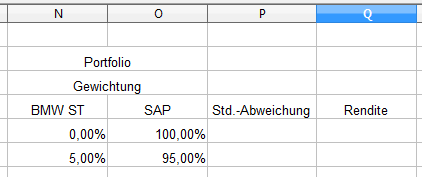Beginnen wollen wir mit dem einfacheren Teil – der Rendite. Die Rendite ist eine lineare Funktion. Ist die Gewichtung beider Aktien beispielweise 50%, so wird 0,5 mal die Rendite der BMW-Aktie berechnet plus 0,5 mal die Rendite der SAP-Aktie. Bei einem Verhältnis von 10% zu 90% wird 0,1 mal die Rendite von BMW plus 0,9 mal die Rendite von SAP berechnet.
In OpenOffice Calc sieht die Funktion wie folgt aus:
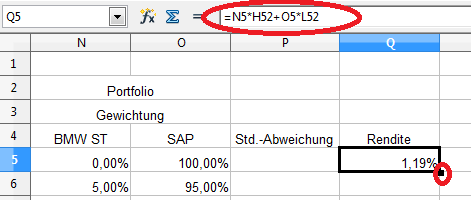In der Formel stehen die Zellen “N5” und “O5” für die Gewichtungen beider Aktienanteile, die Zellen “H52” und “L52” für die mittleren monatlichen Renditen von BMW bzw. SAP.
Da die Gewichtung bei 100% SAP-Anteile liegt, entspricht die Rendite derjenigen der SAP-Aktie.
Für die Ausgabe der Renditen mit den weiteren Gewichtungen müssen wir in die Formel noch etwas bearbeiten. Durch ein “$”-Zeichen vor den Zeilennummern der mittleren, monatlichen Renditen stellen wir sicher, dass immer auf die selbe Zelle zugegriffen wird:
Die Formel hat nun folgenden Inhalt: “=N5*H$52+O5*L$52”.
Jetzt verwenden wir wieder das schwarze Quadrat der markierten, ersten Zelle der Renditeberechung und ziehen es bis zum Ende der Berechnungen.
Die zweite Zelle hat somit folgendes Aussehen:
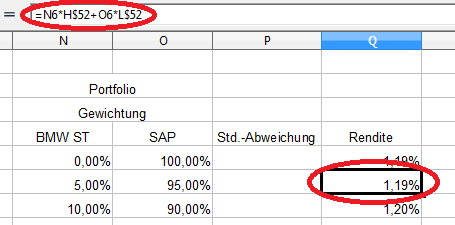Die Gewichtungen werden für die Folgezeilen übernommen, während der Bezug zur Rendite der beiden Wertpapiere gleich bleibt.
Die Formel der Standardabweichung für ein Portfolio aus zwei oder mehr Aktien ist etwas umfangreicher, da keine Linearität zwischen den einzelnen Standardabweichungen besteht (mit einer Ausnahme: Korrelation=1).
Was sich zunächst negativ anhört, ist auf den zweiten Blick ein Glücksfall. Denn nur Dank dieser Tatsache läßt sich das Risiko eines Portfolios bei gleicher Rendite verringern.
Zur Berechnung der Standardabweichung müssen wir den Umweg über die Varianz gehen. Die Formel für den Fall mit zwei Aktien lautet:
Varp = x12 * σ12 + x22 * σ22 + 2 * x1 * x2 * σ1 * σ2 * ρ1,2
Dabei ist
x1, x2 : Gewichtung Aktie 1 und Aktie 2 [0..1]
σ1, σ2 : Standardabweichung Aktie 1 und Aktie 2
ρ1,2 : Korrelation der beiden Aktien [-1..1]
Die Standardabweichung ist die Wurzel der Varianz. In OpenOffice Calc sieht die Formel folgendermaßen aus:
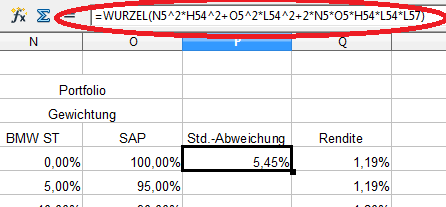N5 und O5 sind die Gewichtungen, H54 und L54 die Standardabweichungen und L57 die Korrelation zwischen der BMW- und der SAP-Aktie.
Jetzt werden wir die Formel wieder mit Konstanten versehen, um die Funktionen für die weiteren Zellen übernehmen zu können. Nicht verändert werden dürfen die Standardabweichungen und die Korrelation:
=WURZEL(N5^2*H$54^2+O5^2*L$54^2+2*N5*O5*H$54*L$54*L$57)
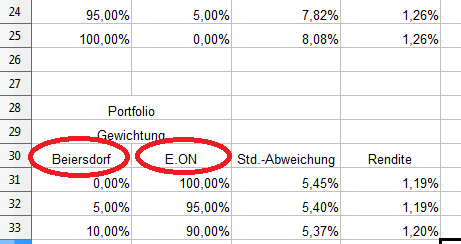
Nach Übernahme der Funktionen über das schwarze Quadrat sehen die Daten wie folgt aus:
Zur besseren Nachvollziebarkeit der Berechnungen sehen Sie nachfolgend noch einen Auszug aus der Tabelle. Durch einen Klick auf die Grafik wird diese vergrößert.
Bild “Berechnungsergebnisse”
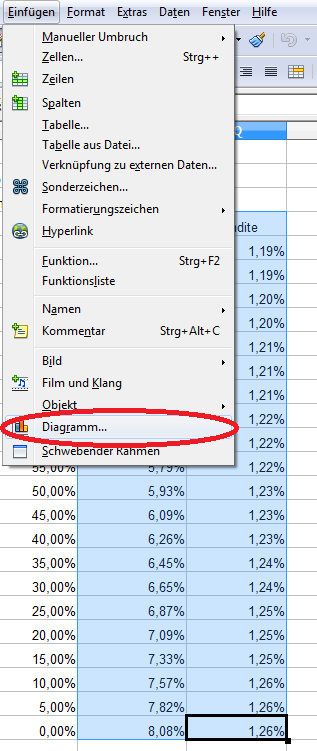
Im nächsten Schritt erstellen wir das Diagramm. Dazu markieren wir die Datenfelder der Standardabweichung und der Rendite inklusive der Überschriften und wählen im Menü “Einfügen” – “Diagramm”.
Es öffnet sich der Diagramm-Assistent, in dem wir folgende Auswahlen treffen:
Als Diagrammtyp verwenden wir das “XY-Streudiagramm” mit Punkten, wobei Sie gerne auch Punke und Linien oder nur Linien auswählen können.
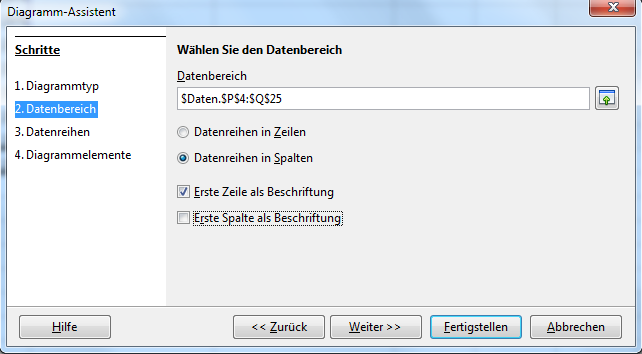
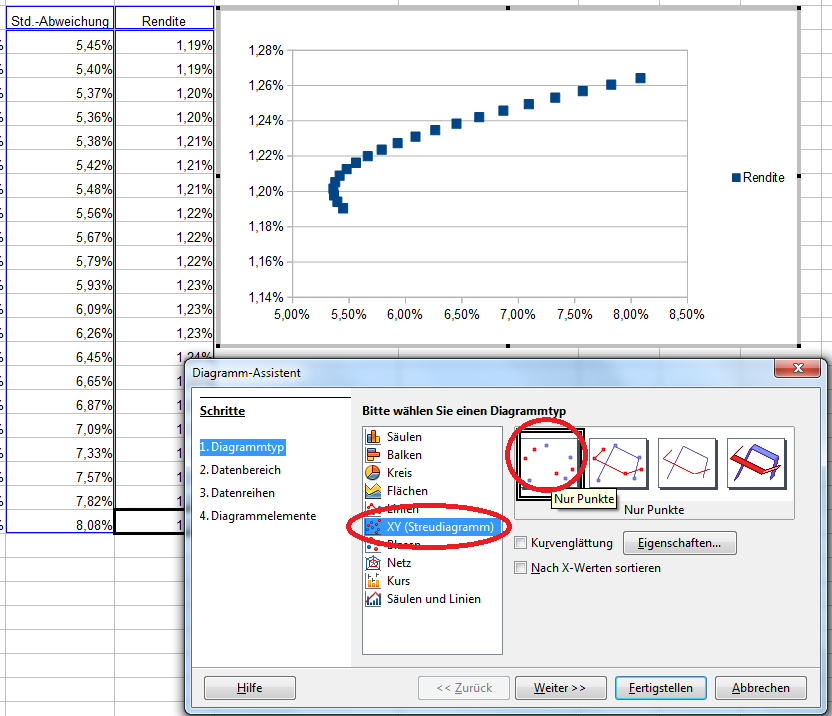Über den “Weiter>>”-Button kommen wir zum Datenbereich. Hier wählen wir “Datenreihen in Spalten” aus.
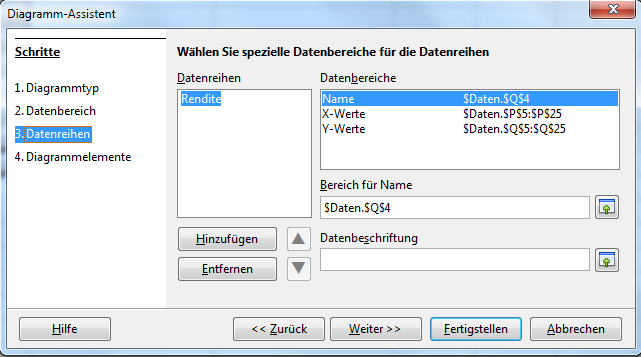
Die Eingaben zum Punkt “Datenreihen” können wir beibehalten.
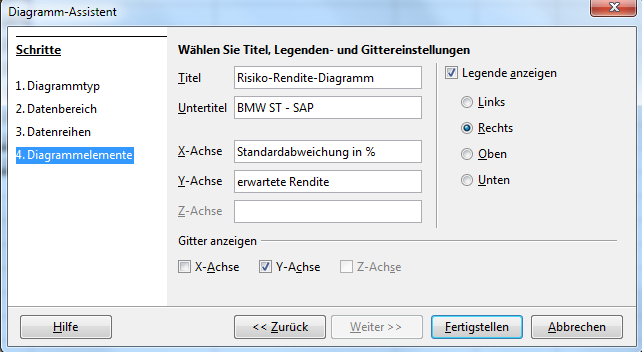
Zuletzt können wir Titel, Untertitel und Legenden beschriften und bei Bedarf die gewünschten Gitter anzeigen.
Das Diagramm sieht dann in der Weise aus:
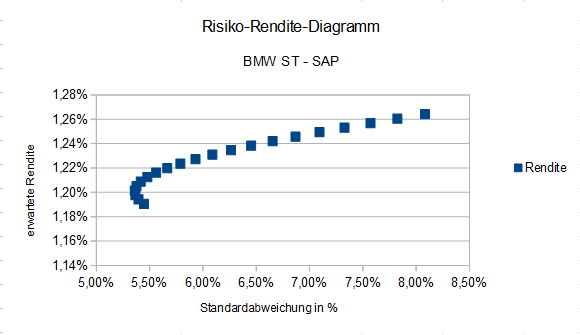Einiges an Arbeit können wir uns bei der Erstellung des zweiten Diagramms sparen, indem wir die Zellen, die wir für das erste Diagramm verwendet haben, kopieren und unterhalb einfügen.
Danach ersetzen wir BMW ST durch Beiersdorf und SAP durch E.ON.
Werfen wir nun einen Blick auf die Risikokomponente, sprich: die Standardabweichung.
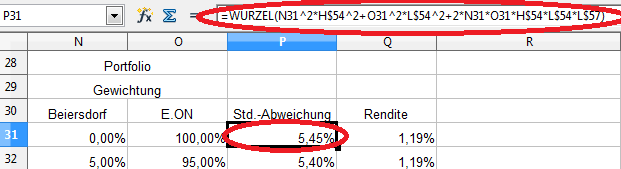Für die Gewichtung sind schon die korrekten Zellen mit “N31” und “O31” übernommen worden. Aber “H$54” weist auf die Standardabweichung von BMW, die durch die Standardabweichung von Beiersdorf (“I$54”) ersetzt werden muss. Gleiches gilt für “L$54” (Standardabweichung von SAP). Dieser Verweis muss auf “K$54” (Standardabweichung E.ON) lauten.
Zuletzt muss die Korrelation “L$57” (Korrelation zwischen BMW SAP) durch die Korrelation zwischen Beiersdorf und E.ON (“K$58”) ersetzt werden.
Die Formel der Bearbeitungsleiste sieht nun folgendermaßen aus:
=WURZEL(N31^2*I$54^2+O31^2*K$54^2+2*N31*O31*I$54*K$54*K$58)
Zum besseren Verständnis der Zellbezüge werfen Sie bitte nochmals einen Blick auf das Bild “Berechnungsergebnisse” weiter oben.
Das gleiche Spiel wiederholen wir für die Rendite:
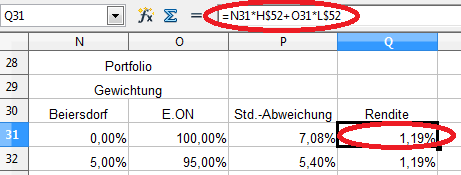Hier müssen wir lediglich die monatliche Rendite von BMW (“H$52”) durch die von Beiersdorf (“I$52”) und die Rendite von SAP (“L$52”) durch die von E.ON (“K$52”) ersetzen:
=N31*I$52+O31*K$52
Nun markieren wir die beiden überarbeiteten Zellen und übernehmen die Daten für die weiteren Felder (schwarzes Quadrat).
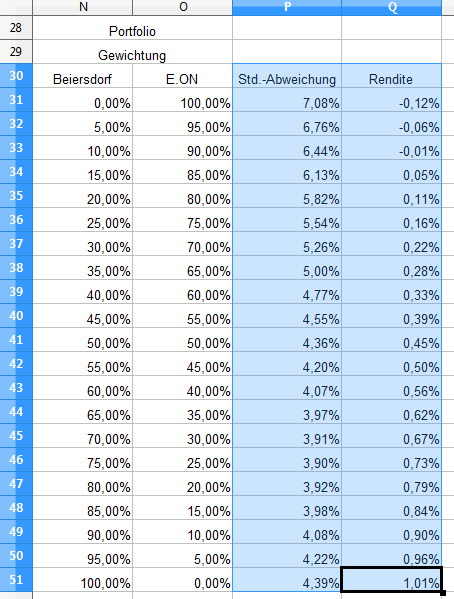Über “Einfügen” – “Diagramm” geben wir das Diagramm mit den Einstellungen von oben aus. Lediglich der Untertitel muss angepaßt werden, da wir ein anderes Aktienpaar verwenden.
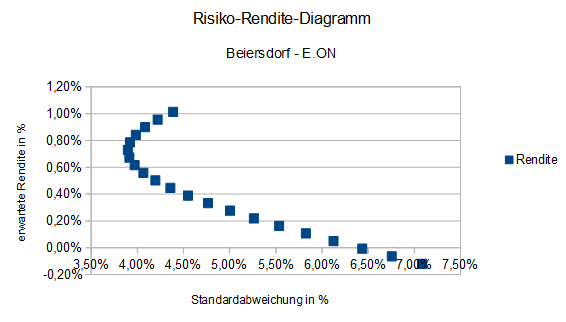Von den fünf Aktien, deren Kurse wir eingelesen haben, können wir im Moment immer nur zwei Aktien im Bezug auf Risiko und Rendite untersuchen. Im nächsten Artikel wollen wir das Portfolio mit allen fünf Aktien überprüfen.
