Der ein oder andere Leser wird sich fragen, was mathematische Wahrscheinlichkeitstheorie in einem Artikel über Aktienstrategien zu suchen hat?

Die Antwort ist schnell gegeben: die Standardabweichung ist ein wichtiges Hilfmittel zur Ermittlung des Risikos einer Anlage.

Über die Standardabweichung und den Mittelwert lässt sich der “Value at Risk” (VaR) berechnen, eine Risikokennzahl, die als Grundlage der beiden in Kürze erscheinenden Strategien “Low-Risk-Index” und “Low-Risk-5”.

Die gute Nachricht vorweg: zur Umsetzung der Strategien sind die nachfolgenden Informationen nicht zwingend erforderlich. Dennoch bin ich überzeugt, dass viele Leser an einer kurzen Herleitung interessiert sind.

Der Mittelwert

Der Mittelwert (englisch: mean) oder auch arithmetisches Mittel (arithmetic mean) ist ein Wert, der uns allen spätestens seit der Schulzeit geläufig ist. Der Notendurchschnitt einer Klassenarbeit ist der Mittelwert aller erzielten Noten.

Dazu ein kleines Beispiel:

Vier Schüler schrieben ein Nacharbeit. Dabei wurden folgende Noten vergeben: je einmal eine 1, eine 2, eine 3 und eine 5. Zur Ermittlung des Notendurchschnitts addieren wir die 4 Noten und teilen sie durch die Anzahl der Benotungen: (1 + 2 + 3 + 5) : 4 = 2,75
Der Notendurchschnitt beträgt also 2,75.

Zu einer weiteren Nacharbeit mussten 8 Schüler antreten. Davon erzielten zwei Schüler eine 1, zwei eine 2, zwei eine 3 und je ein Schüler eine 4 und eine 5:
Unsere Berechnung lautet: (2*1 + 2*2 + 2*3 + 1*4 + 1*5) : 8 = 2,625.

Keine große Hürde – oder?

Warum der Mittelwert als Kenngröße nicht ausreicht

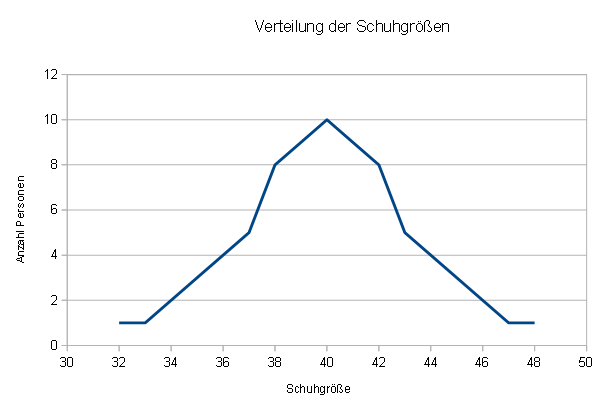
In der nachfolgenden Grafik ist die Verteilung der Schuhgröße von Erwachsenen in einer virtuellen Studie aufgeführt:

Der Mittelwert der Schuhgröße wurde mit 40 errechnet, was sich auch gut in der Grafik erkennen lässt.

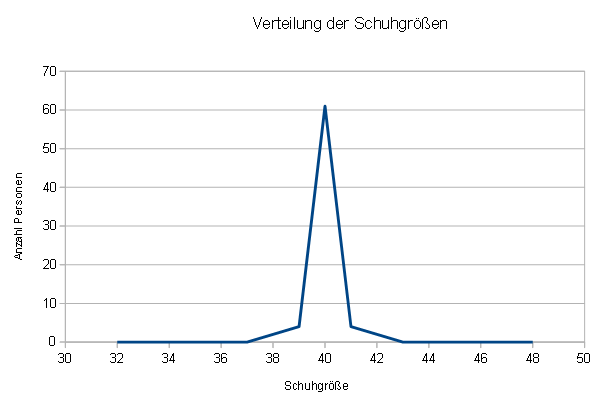
In der nächsten Grafik haben wir ebenfalls einen Mittelwert von 40. Werfen wir einen Blick darauf:

Obwohl der Mittelwert beider Grafiken gleich ist, fällt auf, dass die Werte in der zweiten Grafik viel näher am Mittelwert liegen als in der ersten Grafik. Die Standardabweichung (Streuung) ist in der zweiten Grafik geringer.

Für einen Schuhfabrikanten bedeutet dies eine äußerst wertvolle Information. Wäre die zweite Grafik gültig, so müsste er nur Schuhe der Größen 38 bis 42 mit Schwerpunkt auf Größe 40 produzieren.

Und für den Anleger ist die Information, ob eine Aktie, die bei 40 € notiert, mit einer gewissen Wahrscheinlichkeit auf 20 € oder nur auf 39 € fallen kann, nicht weniger aufschlußreich.

 Die Varianz

Die Standardabweichung (englisch:standard deviation) setzt sich aus den Abweichungen der einzelnen Werte im Bezug zum Mittelwert geteilt durch die Anzahl der Werte zusammen. Angenommen wir haben die Werte 3,8 – 3,9 – 4,0 – 4,1 und 4,2.
Der Mittelwert ist 4,0, wie schon auf den ersten Blick zu erkennen ist. Nun lassen Sie uns die Abweichungen addieren:
(3,8 – 4,0) + (3,9 – 4,0) + (4,0 – 4,0) + (4,1 – 4,0) + (4,2 – 4,0)
= -0,2 -0,1 + 0,0 + 0,1 + 0,2 = 0,0

Bei einer symmetrischen Verteilung wäre die Abweichung immer 0, unabhängig wie weit die Werte streuen. Das ist definitiv nicht das gesuchte Ergebnis.

Die Varianz (englisch: variance) ist nun einfach eine Hilfsberechnung, um den oben erkannten Mangel auszubügeln. Die Ausdrücke in den Klammern (Istwert minus Mittelwert) werden quadriert und erzeugen somit nur positive Werte. Berechnen wir die Varianz des oberen Beispiels:
(3,8 – 4,0)² + (3,9 – 4,0)² + (4,0 – 4,0)² + (4,1 – 4,0)² + (4,2 – 4,0)²

= 0,04 + 0,01 + 0 + 0,01 + 0,04 = 0,1

Die Zahl muss noch durch die Anzahl dert Werte geteilt werden, um zum Ergebnis zu gelangen:
= 0,1 : 5 = 0,02

Wie erwartet heben sich die Werte nicht mehr gegenseitig auf. Bei einer großen Abweichung zum Mittelwert erhalten wir einen großen Wert der Varianz, bei kleinen Abweichungen einen kleinen Wert.

Hier noch die Berechnung der Varianz als Formel:

Var =((x₁ – x_m)² + (x₂ – x_m)² + (x₃ – x_m)² + … + (x_n – x_m)²) : n

x₁ … x_n stellen die einzelnen Werte dar

x_m ist der Mittelwert

n ist die Anzahl aller Werte

Die Standardabweichung

Warum nicht einfach die Varianz zur Ermittlung der Streuung verwendet wird, um einen Rechenschritt zu sparen, soll folgendes Beispiel zeigen:

Die Größe dreier Personen beträgt 170 cm, 175 cm und 180 cm. Somit liegt der Mittelwert bei 175 cm und wir können die Varianz berechnen:

((170 cm – 175 cm)² + (175 cm – 175 cm)² + (180 cm – 175 cm)²) : 3

= (25 cm² + 0 cm² + 25 cm²) : 3 = 16,66 cm²

Das Ergebnis ist in Quadratzentimetern angegeben. Der Bezug ist jedoch keine Fläche, sondern eine eindimensionale Größe. Um also wieder zur Bezugseinheit zu gelangen, muss die Wurzel der Varianz gebildet werden:

Die Formel für die Standardabweichung σ lautet:

Was sagt der Wert der Standardabweichung eigentlich aus?

Wie bereits erwähnt, kommt der Begriff aus der Wahrscheinlichkeitsrechnung. Die Standardabweichung von 4,08 cm sagt aus, dass bei einer Normalverteilung 68,3 % aller Werte im Bereich zwischen 171,92 cm (x_m – σ) und 179,08 cm (x_m + σ) liegen. 95,5 % aller Werte liegen im Bereich +- 2σ (zwischen 166,84 cm und 183,16 cm) und 99,7 % aller Werte liegen zwischen +- 3σ (162,76 cm bis 187,24 cm).

Bitte beachten Sie, dass es sich hierbei nur um konstruierte Werte handelt. In Realität ist die Streuung breiter.

Im nächsten Kapitel “Value-at-Risk” wird beschrieben, wie sich der Sachverhalt auf Aktien umlegen lässt.