 Im letzten Artikel wurden Risiko und Rendite eines Portfolios mit fünf Aktien berechnet. Dabei wurden alle Aktien mit 20% gewichtet.
Im letzten Artikel wurden Risiko und Rendite eines Portfolios mit fünf Aktien berechnet. Dabei wurden alle Aktien mit 20% gewichtet.
Zur Portfolio-Optimierung müssen – je nach persönlichem Ziel – die einzelnen Komponenten unterschiedlich gewichtet sein.
Natürlich können Sie einfach unterschiedliche Werte ausprobieren und das Ergebnis betrachten. Wirklich effektiv ist diese Methode jedoch nicht, wie folgendes Beispiel erkennen läßt:
In einer früheren Auswertung mit einem anderen Portfolio wurden alle Möglichkeiten der Gewichtung in 10%-Stufen festgelegt.
In OpenOffice Calc sieht der Aufbau folgendermaßen aus:
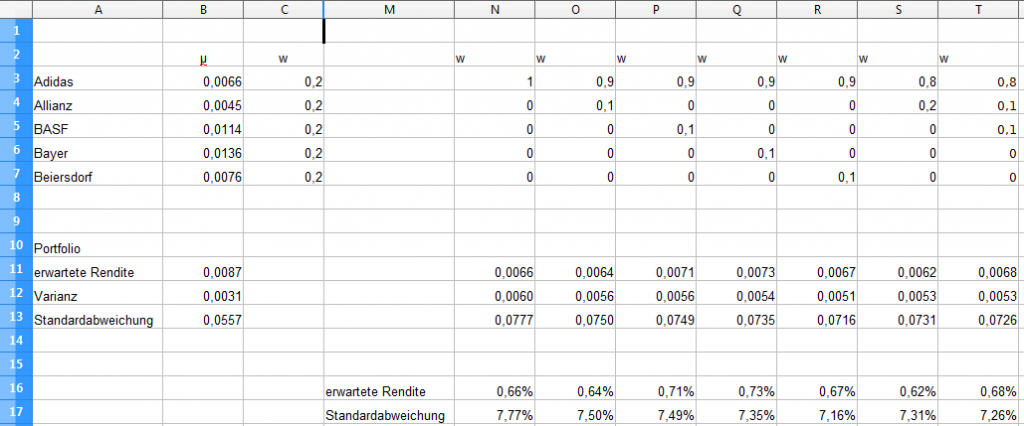 In Spalte „N“ besteht das Portfolio zu 100% aus Adidas-Aktien. In Spalte „O“ beträgt der Anteil der Adidas-Aktien 90%, hinzu kommen 10% Allianz-Aktien.
In Spalte „N“ besteht das Portfolio zu 100% aus Adidas-Aktien. In Spalte „O“ beträgt der Anteil der Adidas-Aktien 90%, hinzu kommen 10% Allianz-Aktien.
Um alle Varianten auszuspielen, werden mehr als 1000 Spalten benötigt. Dabei ist die Schrittweite von 10% für die praktische Umsetzung zu groß. Wollen wir eine geringere Schrittweite von beispielsweise 1% oder eine Portfolio mit mehr Einzelwerten, ist diese Art der Auswertung nicht mehr zu bewältigen.
Wesentlich geeigneter für das Arbeiten mit unterschiedlichen Gewichtungen ist die Monte-Carlo-Simulation, die bereits im Zusammenhang mit dem „Value at Risk„ erwähnt wurde.
Bei der Monte-Carlo-Simulation werden Zufallszahlen für die jeweiligen Anteile des Portfoliobestandes gebildet. Dabei muss die Bedingung erfüllt sein, dass alle Anteile zusammen 100% ergeben.
Von diesen Zufallsreihen werden nun etliche Tausende ermittelt, um eine ausreichende Anzahl an Variationen zur Verfügung zu haben.
Die Datenreihen samt Ergebnissen im Bezug auf Risiko und Rendite können danach auf die gewünschten Informationen hin gefiltert und ausgewertet werden.
Zu einem späteren Zeitpunkt werden wir diese Methode in einem separaten Artikel umsetzen.
Portfolio-Optimierung mit dem Solver
Moderne Tabellenkalkulationsprogramme wie Excel und OpenOffice Calc bieten mit dem „Solver“ ein mächtiges Tool an. Der „Solver“ (deutsch: Löser) ist eine erweiterte Zielwertsuche, bei der der gesuchte Wert in Abhängigkeit von mehreren Nebenbedingungen ermittelt werden kann.
In Excel steht der „Solver“ als „Add-In“ zur Verfügung, welches unter „Extras“ / „Add-Ins“ vor dem ersten Einsatz installiert werden muss.
OpenOffice Calc stellt standardmäßig einen „Solver“ bei, allerdings nur für lineare Gleichungssysteme. Um alle Möglichkeiten nutzen zu können, müssen wir eine Extension für nichtlineare Gleichungssysteme nachrüsten.
Wir wollen den kostenlosen „Solver for Nonlinear Programming [Beta]“ einsetzen, der hier zum Download zur Verfügung steht.
 Nach einem Klick auf den Button „Download extension“ öffnet sich eine neue Seite, in der folgende Dialogbox erscheint:
Nach einem Klick auf den Button „Download extension“ öffnet sich eine neue Seite, in der folgende Dialogbox erscheint:
 Am einfachsten lässt sich die Installation über die Auswahl „Öffnen mit OpenOffice“ durchführen. Die Extension wird automatisch in OpenOffice eingebunden.
Am einfachsten lässt sich die Installation über die Auswahl „Öffnen mit OpenOffice“ durchführen. Die Extension wird automatisch in OpenOffice eingebunden.
Aufgerufen wird der „Solver“ über „Extras“ / „Sover“.
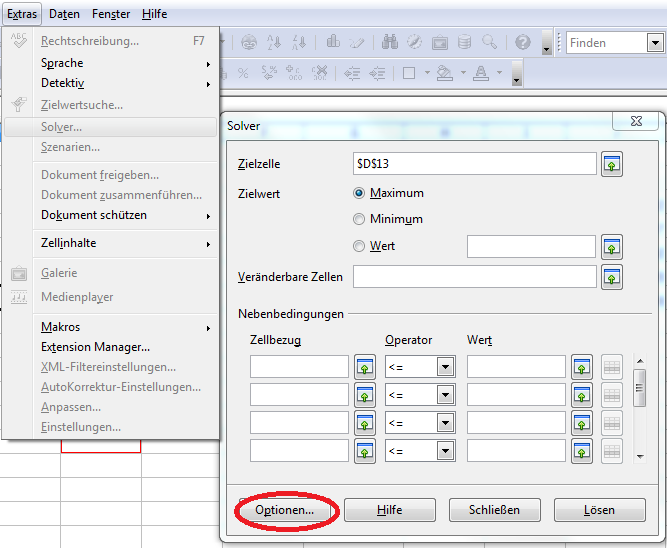 Zum Prüfen, ob die Extension installiert wurde, gehen Sie auf „Optionen“ und öffnen das Listenfeld unter „Solver Engine“. Hier müssen nun drei „Solver“ zur Auswahl stehen.
Zum Prüfen, ob die Extension installiert wurde, gehen Sie auf „Optionen“ und öffnen das Listenfeld unter „Solver Engine“. Hier müssen nun drei „Solver“ zur Auswahl stehen.
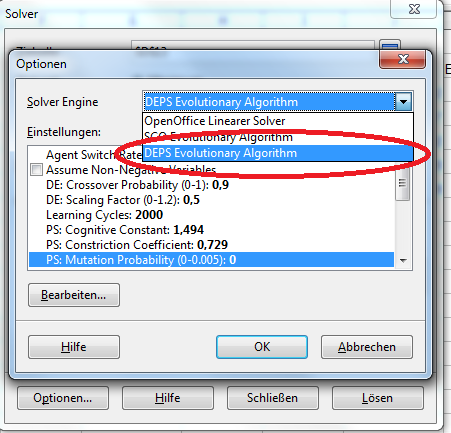 Wählen Sie den „DEPS Evolutionary Algorithm“ aus.
Wählen Sie den „DEPS Evolutionary Algorithm“ aus.
Für die weiteren Ausführungen verwenden wir wieder die im letzten Artikel erstellte Datei „Portfolio_5_Aktien.ods“.
Bevor wir mit dem Solver fortfahren, müssen wir in der Tabelle „Berechnung“ noch ein Feld ergänzen.
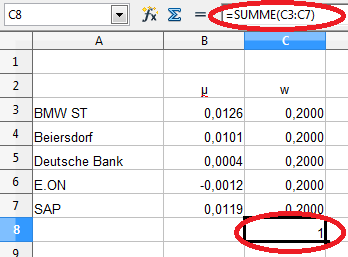 Eine Voraussetzung, die wir im „Solver“ einsetzen, ist, dass die Summe aller Gewichtungen „1“ (100%) ergibt. Diese Berechnung führen wir in der Zelle C8 aus.
Eine Voraussetzung, die wir im „Solver“ einsetzen, ist, dass die Summe aller Gewichtungen „1“ (100%) ergibt. Diese Berechnung führen wir in der Zelle C8 aus.
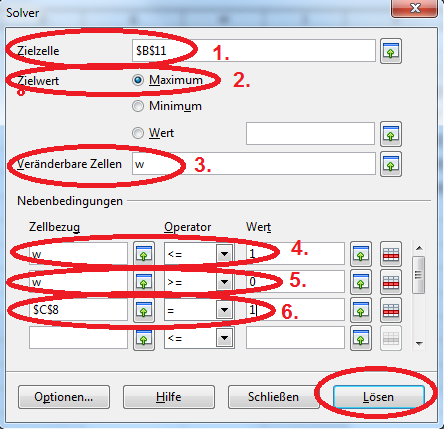
Nun wollen wir den „Solver“ einsetzen. Die erste Aufgabe soll die Bestimmung der größten zu erwartenden Rendite sein.
Dazu starten wir den „Solver“ über „Extras“ / „Sover“ und machen folgende Eingaben, bzw. Vorwahlen:
- Die Zielzelle beinhaltet den Wert, den wir beeinflussen wollen. In diesem Fall ist es die Rendite.
- Zielwert ist das Maximum, da wir die höchste Rendite suchen.
- Die veränderbaren Zellen sind die jeweiligen Gewichtungen (C3:C7 oder als Name „w“), da wir wissen wollen, bei welchen Gewichtungen die höchste Rendite zu erwarten ist.
- Als erste Nebenbedingung definieren wir, dass die einzelnen Anteile nicht größer als „1“ (100%) sein dürfen.
- Als zweite Nebenbedingung legen wir fest, dass die einzelnen Anteile nicht negativ sein dürfen. Prinzipiell sind auch negative Werte bis „-1“ möglich. In diesem Fall würde mit Verkaufsoptionen gearbeitet. Da es zu vielen Papieren aber keine entsprechenden Verkaufsoptionen gibt, bzw. nicht jeder Zugang zu dieser Art von Wertpapieren hat, verzichten wir auf diese Variante.
- Als dritte Nebenbedingung wird bestimmt, dass die Summe der Gewichtungen „1“ (100%) betragen muss.
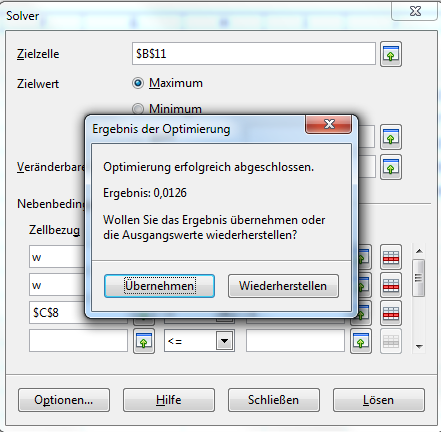
Zur Ausgabe des Ergebnisses drücken Sie den Button „Lösen“. Der „Solver“ führt die Berechnungen aus.
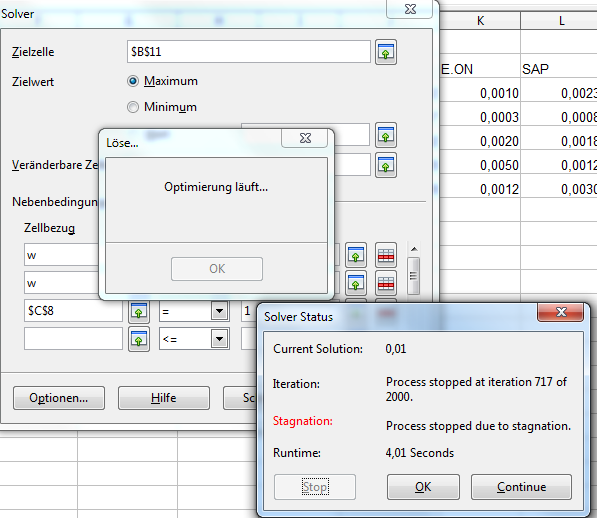 Mit „OK“ wird die Berechnung abgeschlossen und Sie werden gefragt, ob Sie die Ergebnisse in Ihre Tabelle übernehmen wollen.
Mit „OK“ wird die Berechnung abgeschlossen und Sie werden gefragt, ob Sie die Ergebnisse in Ihre Tabelle übernehmen wollen.
Werfen wir einen Blick auf das Ergebnis:
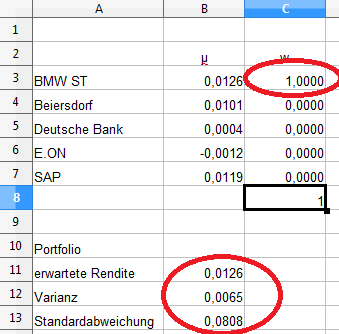 Als Resultat erhalten wir ein Portfolio, das zu 100% aus BMW-Aktien besteht. Das Ergebnis kann nicht wirklich überraschen, wenn wir uns daran erinnern, dass die Rendite eine lineare Funktion ist. Die höchste Rendite erzielen wir, wenn wir nur den Wert mit der höchsten Rendite einsetzen.
Als Resultat erhalten wir ein Portfolio, das zu 100% aus BMW-Aktien besteht. Das Ergebnis kann nicht wirklich überraschen, wenn wir uns daran erinnern, dass die Rendite eine lineare Funktion ist. Die höchste Rendite erzielen wir, wenn wir nur den Wert mit der höchsten Rendite einsetzen.
Aber Ziel der Portfolio-Theorie ist die Reduzierung des Risikos bei akzeptabler Rendite. Mit nur einem Titel tragen wir jedoch das komplette, unsystematische (diversifizierbare) Risiko.
Minimum-Varianz Portfolio
Als Nächstes wollen wir das Minimum-Varianz Portfolio (MVP) bestimmen. Das MVP ist das Portfolio mit dem geringsten Risiko.
Dazu öffnen wir erneut den „Solver“ und ändern zwei Werte.
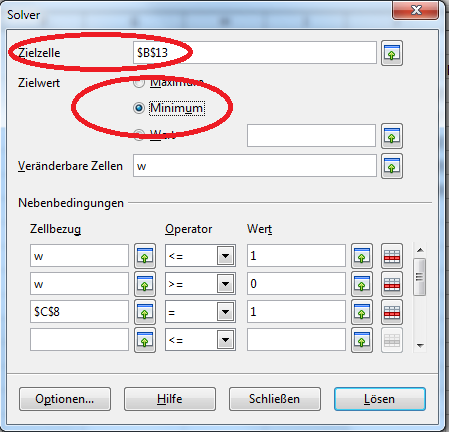 Zunächst wählen wir als Zielzelle die Standardabweichung (Zelle B13). Die Varianz wäre als Zielzelle ebenfalls möglich, da Standardabweichung und Varianz in direktem Zusammenhang stehen.
Zunächst wählen wir als Zielzelle die Standardabweichung (Zelle B13). Die Varianz wäre als Zielzelle ebenfalls möglich, da Standardabweichung und Varianz in direktem Zusammenhang stehen.
Die zweite Änderung betrifft den Zielwert. Hier wählen wir „Minimum“, da der kleinste Wert gesucht wird.
Nach Lösen der Gleichung und Durchlauf aller 2000 Berechnungsschritte erhalten wir folgendes Ergebnis.
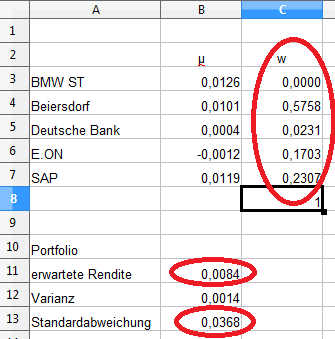 Durch die Änderung der Gewichtung in 0% BMW, 57,58% Beiersdorf, 2,31% Deutsche Bank, 17,03% E.ON und 23,07% SAP kann das Risiko von 8,08% auf 3,68% mehr als halbiert werden. Gleichzeitig sinkt die Rendite um weniger als ein Drittel.
Durch die Änderung der Gewichtung in 0% BMW, 57,58% Beiersdorf, 2,31% Deutsche Bank, 17,03% E.ON und 23,07% SAP kann das Risiko von 8,08% auf 3,68% mehr als halbiert werden. Gleichzeitig sinkt die Rendite um weniger als ein Drittel.
Der effiziente Rand
Der effiziente Rand beschreibt die Kurve vom Minimum-Varianz Portfolio zum Portfolio mit der höchsten Rendite für die zu jedem Wert der Standardabweichung keine höhere Rendite möglich ist.
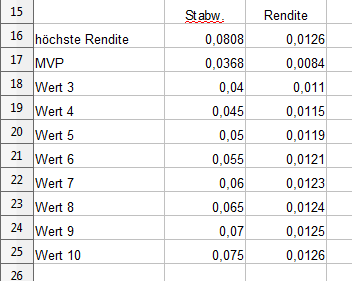
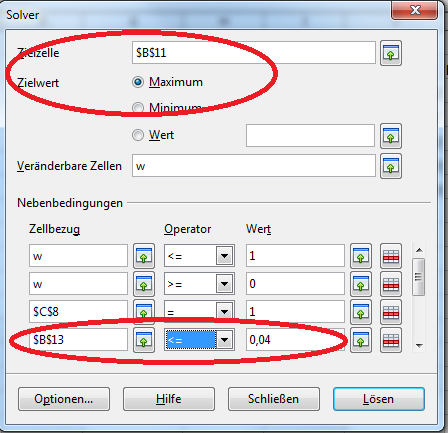
Wir wollen nun den effizienten Rand unseres Portfolios bestimmen. Dazu tragen wir einmal die Standardabweichung und die Rendite für das Portfolio mit der höchsten Rendite ein, danach die Werte des MVP.
Jetzt haben wir die äußeren Begrenzungen der Kurve. Weitere Punkte legen wir fest, indem wir für die Standardabweichungen 0,04 – 0,045 – 0,05 etc. bis 0,075 die höchsten Renditen berechnen.
Dafür wählen wir wieder die Rendite als Zielzelle und „Maximum“ als Zielwert. Als vierte Nebenbedingung fügen wir den gewünschten Sollwert der Standardabweichung hinzu. Allerdings verwenden wir nicht den Operator „=“ sondern „<=“. Bei „=“ wird ganz genau der Wert „0,4000000“ gefordert, was u.U. zu keiner Lösung führt.
Die Berechnungen werden für alle Werte der vorgegebenen Standardabweichungen ausgeführt und die Werte in der Tabelle ergänzt.
 Den besten Überblick bietet ein Diagramm. Unter „Einfügen“ / „Diagramm“ wird das Streudiagramm ausgewählt. Wir erhalten folgendes Ergebnis:
Den besten Überblick bietet ein Diagramm. Unter „Einfügen“ / „Diagramm“ wird das Streudiagramm ausgewählt. Wir erhalten folgendes Ergebnis:
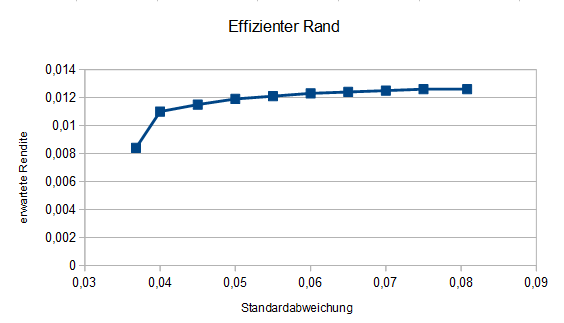 Je mehr Zwischenwerte errechnet werden, desto genauer wird die Kurve.
Je mehr Zwischenwerte errechnet werden, desto genauer wird die Kurve.
Allerdings läßt sich schon deutlich erkennen, dass nach dem linken Punkt (MVP) ein steiler Anstieg der Rendite erfolgt, der im weiteren Verlauf immer mehr abflacht.
Das bedeutet, dass im Bereich der Standardabweichung von 0,04 bis 0,05 ein sehr gutes Chance-Risiko Verhältnis für dieses Portfolio besteht. Danach werden kleine Renditesprünge mit deutlicher Erhöhung des Risikos erkauft.
Hinweis:
Der Artikel beschreibt nur die Möglichkeit, wie die Optimierung eines Portfolios mit dem „Solver“ durchgeführt werden kann.
Wer sich der Portfolio-Theorie verschreibt, wird nie ein Portfolio aufbauen, das nur aus Werten des DAX besteht.
Bei einer größeren Anlagesumme besteht die Möglichkeit eine Diversifikation durch Aktien unterschiedlicher Branchen, Regionen und Marktkapitalisierungen. Neben der notwendigen Kapitalbasis ist hierfür auch ein entsprechender Zeitaufwand zu kalkulieren.
Einfacher und mit weniger Startkapital lässt sich ein optimiertes Portfolio mit ETFs, Index- und Themenzertifikaten und Fonds (etwas kostspieliger) umsetzen.
Je nach Risikoneigung sollten auch Anleihen mit hoher Bonität zur Senkung des Risikos eingesetzt werden.



3 Kommentare
1 Ping
Hallo, schönes Beispiel, werde Ich mal nachzuvollziehen ersuchen.
Gruß von Lothar Feige
Hallo Herr Maier,
gibt es dafür eine App?
Gruß von Lothar Feige
Autor
Hallo Herr Feige,
mir wäre jetzt keine kostenlose App in deutscher Sprache bekannt.
In englischer Sprache gibt es ein paar Online Tools, die ich aber selbst nicht einsetze und entsprechend nicht beurteilen kann.
Ich kann über Ostern mal schauen, ob ich noch etwas finde.
Gruß Mathias
[…] müssen die Ergebnisse für verschiedene Gewichtungen der Einzelwerte vorgenommen werden. In einem früheren Artikel zum Thema wurde festgestellt, dass bei einem Portfolio aus 5 verschiedenen Wertpapieren mit einer […]