 Für die Portfolio-Optimierung müssen die Ergebnisse für verschiedene Gewichtungen der Einzelwerte vorgenommen werden. In einem früheren Artikel zum Thema wurde festgestellt, dass bei einem Portfolio aus 5 verschiedenen Wertpapieren mit einer Veränderung der Gewichtung in 10%-Stufen bereits mehr als 1000 Variationen vorgegeben werden müssen.
Für die Portfolio-Optimierung müssen die Ergebnisse für verschiedene Gewichtungen der Einzelwerte vorgenommen werden. In einem früheren Artikel zum Thema wurde festgestellt, dass bei einem Portfolio aus 5 verschiedenen Wertpapieren mit einer Veränderung der Gewichtung in 10%-Stufen bereits mehr als 1000 Variationen vorgegeben werden müssen.
Mit einer Monte-Carlo-Simulation lässt sich das Problem einfacher lösen. Die entsprechende Umsetzung soll Thema dieses Artikels sein.
Zwar wird die Vorgehensweise nochmals komplett vorgestellt, aber nicht so detailliert wie in der Artikelserie zu den Portfolios, bzw. der Matrix-Algebra.
Sollten einige Punkte unklar sein, so werfen Sie bitte einen Blick in die entsprechenden Artikel, die Sie unter dem Menüpunkt “Wissen” (Artikel 9 bis 15) finden können. Selbstverständlich können Sie Ihre Fragen auch über die Kommentarfunktion stellen.
Soweit Unterschiede zu den Artikeln vorhanden sein sollten, werden diese explizit angesprochen.
Schritt 1: Kursdaten einlesen
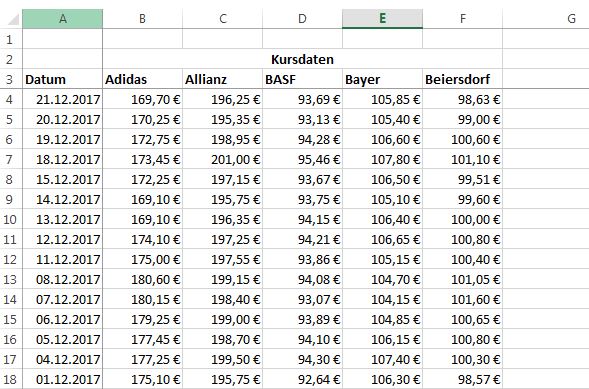
Zu Beginn werden die Kursdaten der ausgewählten Aktien benötigt. In dem Beispiel wurden mit Adidas, Allianz, BASF, Bayer und Beiersdorf die fünf alphabetisch ersten Aktien verwendet. Dazu wurden die jeweiligen Tagesschlusskurse vom 21.12.2016 bis 21.12.2017 heruntergeladen und in die Tabelle “Daten” eingefügt (siehe Artikel Korrelation mit OpenOffice Calc berechnen).
 Schritt 2: Tägliche Renditen berechnen
Schritt 2: Tägliche Renditen berechnen
Aus den Kursdaten werden die täglichen Renditen berechnet.
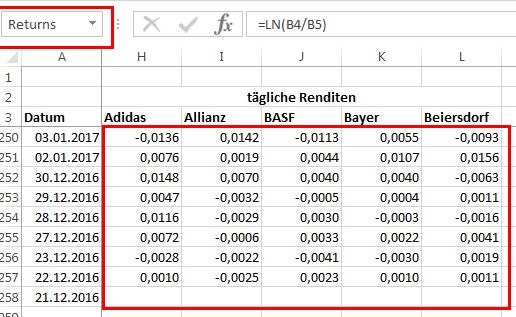
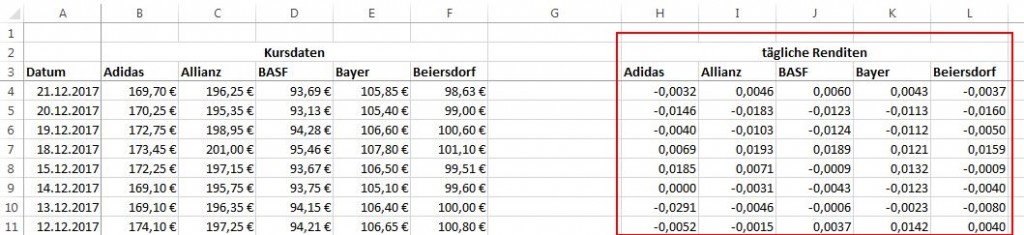 Bitte beachten Sie, dass im Gegensatz zum ursprünglichen Artikel nicht mit der Formel “=(Wert1-Wert2)/Wert2” für die Berechnung von diskreten Renditen, sondern mit der Formel “=LN(Wert1/Wert2)” für die Berechnung stetiger Renditen gearbeitet wird.
Bitte beachten Sie, dass im Gegensatz zum ursprünglichen Artikel nicht mit der Formel “=(Wert1-Wert2)/Wert2” für die Berechnung von diskreten Renditen, sondern mit der Formel “=LN(Wert1/Wert2)” für die Berechnung stetiger Renditen gearbeitet wird.
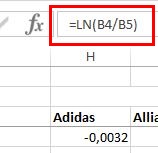 Für Interessierte gibt es <hier> ein schönes Erklärungsvideo zu dem Thema. Die Unterschiede im Ergebnis sind nicht groß, wie im nächsten Bild zu erkennen ist, können sich aber aufaddieren.
Für Interessierte gibt es <hier> ein schönes Erklärungsvideo zu dem Thema. Die Unterschiede im Ergebnis sind nicht groß, wie im nächsten Bild zu erkennen ist, können sich aber aufaddieren.
 Zu erkennen ist auch, dass die in unserer Berechnung verwendete Formel “=LN(Wert1/Wert2)” gleichzusetzen ist mit der Formel “=LN(Wert1) – LN(Wert2)”, die im Video verwendet wird.
Zu erkennen ist auch, dass die in unserer Berechnung verwendete Formel “=LN(Wert1/Wert2)” gleichzusetzen ist mit der Formel “=LN(Wert1) – LN(Wert2)”, die im Video verwendet wird.
Zum Abschluss werden alle Zellen H4 bis L257 markiert und der Name “Returns” für den Zellbereich vergeben.
Schritt 3: Rendite der Aktien berechnen
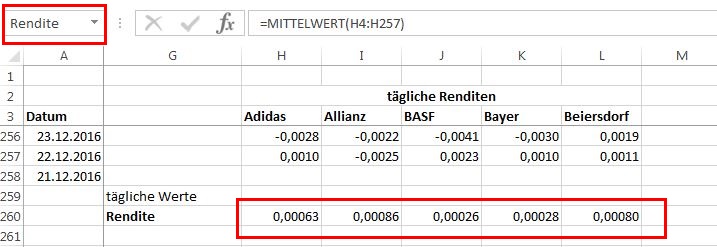
Für jede der einzelnen Aktien wird nun der Mittelwert der täglichen Renditen gebildet.
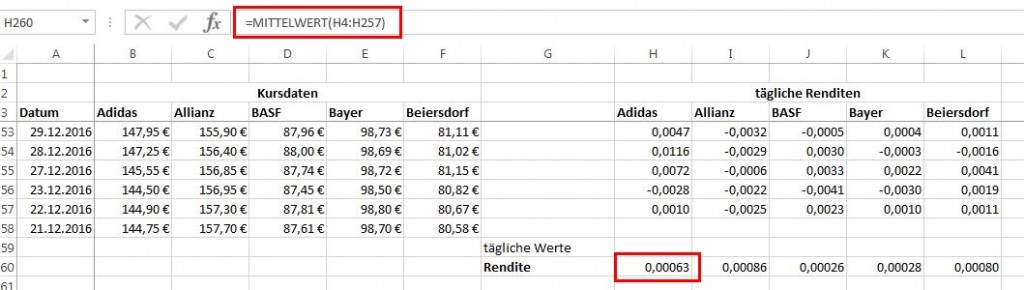 Danach werden die fünf Zellen markiert und der Name “Rendite” für den Zellbereich vergeben.
Danach werden die fünf Zellen markiert und der Name “Rendite” für den Zellbereich vergeben.
 Schritt 4: Berechnung der täglichen Renditen bezogen auf den Mittelwert
Schritt 4: Berechnung der täglichen Renditen bezogen auf den Mittelwert
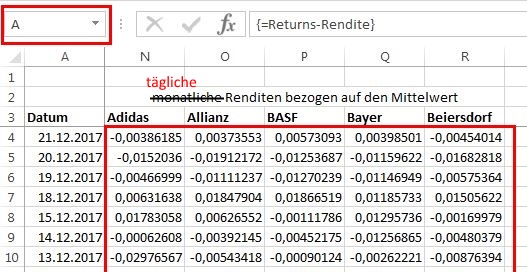
Die folgende Vorgehensweise ist in diesem Artikel detaillierter erklärt. Nach Einfügen der Spaltenüberschriften werden die Zellen N4 bis R257 markiert. Anschließend wird die Formel “=Returns-Rendite” eingetragen. Da es sich um eine Matrix-Berechnung handelt, muss die Formel mit “<Strg>+<Shift>+<ENTER>” abgeschlossen werden, wodurch die Formel in einer geschweiften Klammer dargestellt wird.
 Nun wird dem Zellbereich N4 bis R257 noch der Name “A” zugewiesen.
Nun wird dem Zellbereich N4 bis R257 noch der Name “A” zugewiesen.
 Schritt 5: Tabelle “Berechnung” anlegen und Renditewerte übernehmen
Schritt 5: Tabelle “Berechnung” anlegen und Renditewerte übernehmen
Nun wird eine neue Tabelle mit dem Namen “Berechnung” angelegt. Danach tragen wir nochmals die im Tabellenblatt “Daten” errechnete Rendite ein, indem die fünf Zellen markiert werden, die Formel “=MTRANS(Rendite)” eingetragen und mit “<Strg>+<Shift>+<ENTER>” abgeschlossen wird. Zuletzt wird der Name “mue” für die fünf Zellen vergeben.
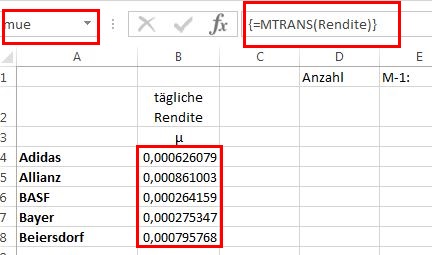 Der zusätzliche Eintrag der Rendite in dieses Tabellenblatt ist nicht notwendig, sondern wurde nur in Anlehnung an die früheren Artikel vorgenommen.
Der zusätzliche Eintrag der Rendite in dieses Tabellenblatt ist nicht notwendig, sondern wurde nur in Anlehnung an die früheren Artikel vorgenommen.
Schritt 6: Berechnung der Varianz-Kovarianz Matrix
Zur späteren Berechnung der Varianz und in Folge der Standardabweichung wird die Varianz-Kovarianz Matrix benötigt, die wie folgt definiert ist:
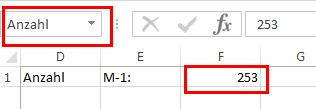
“A” ist die Matrix mit den monatlichen Renditen bezogen auf den Mittelwert, die in Schritt 4 erstellt wurde. M -1 ist die Anzahl der beobachteten periodischen Renditen. Da 254 periodische Datenreihen vorliegen, beträgt der Wert für M-1 253. Dieser Zelle wird nun der Name “Anzahl” zugewiesen, der in der Formel anstelle von M-1 verwendet wird.
 Um die Varianz-Kovarianz Matrix zu erstellen, werden horizontal und vertikal die Namen der Aktien eingetragen. Die 5×5 Felder dazwischen werden mit der Formel “=MMULT(MTRANS(A);A)/Anzahl” gefüllt und mit “<Strg>+<Shift>+<ENTER>” abgeschlossen. Als Name für die Matrix wird “_S” vergeben, da “S” von Excel nicht akzeptiert wird.
Um die Varianz-Kovarianz Matrix zu erstellen, werden horizontal und vertikal die Namen der Aktien eingetragen. Die 5×5 Felder dazwischen werden mit der Formel “=MMULT(MTRANS(A);A)/Anzahl” gefüllt und mit “<Strg>+<Shift>+<ENTER>” abgeschlossen. Als Name für die Matrix wird “_S” vergeben, da “S” von Excel nicht akzeptiert wird. 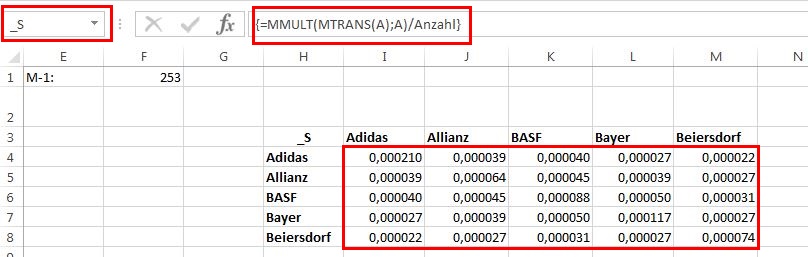 Schritt 7: Zufallszahlen für die Gewichtung erzeugen
Schritt 7: Zufallszahlen für die Gewichtung erzeugen
In der Monte-Carlo-Simulation werden Zufallszahlen in großer Anzahl eingesetzt. Für dieses Beispiel betreffen die Zufallszahlen die Gewichtung der einzelnen Aktien innerhalb des Portfolios. Das wirft ein Problem auf, schließlich können keine beliebigen Zufallszahlen verwendet werden, da die Summe immer “1” (also 100%) ergeben muss.
Dafür gibt es zwei einfache Lösungen, die nun genauer untersucht werden sollen.
Bei der ersten Möglichkeit wird die Summe aller einzelnen Zufallszahlen gebildet, danach werden die einzelnen Zufallszahlen durch diese Summe geteilt und mit der gewünschten Endsumme multipliziert.
Z.B. fünf Zufallszahlen aus dem Bereich 0 bis 100 sollen zusammen 100 ergeben. Die einzelnen Zufallszahlen lauten 20, 30, 40, 50, 60. Die Summe aller Zufallszahlen ist also 200.
1.Zufallszahl: 20 / 200 * 100 = 10
2.Zufallszahl: 30 / 200 * 100 = 15
3.Zufallszahl: 40 / 200 * 100 = 20
4.Zufallszahl: 50 / 200 * 100 = 25
5.Zufallszahl: 60 / 200 * 100 = 30
Die Summe aller fünf angepassten Zufallszahlen ergibt wie gewünscht 100. Werfen wir einen Blick auf die Verteilung der einzelnen Zufallszahlen: 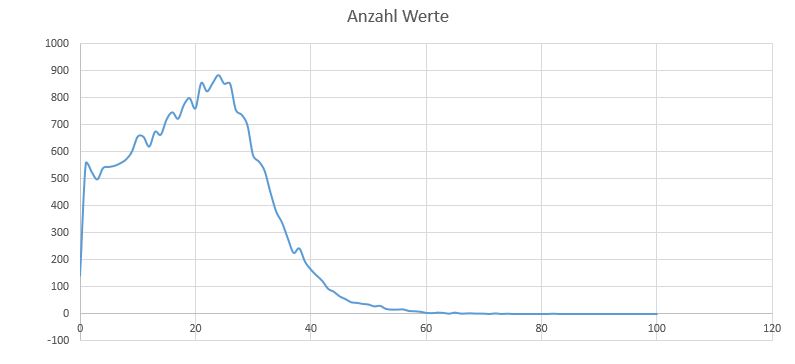
< Diagramm Verteilung Variante 1>
Die meisten Zufallszahlen finden sich im Bereich zwischen 20 und 30. Das wäre kein Problem, doch über 80 finden sich so gut wie keine Werte mehr. Ein vernünftiges Ergebnis ist mit dieser Methode nicht zu erwarten.
Bei der zweiten Möglichkeit wird für den ersten Wert eine Zufallszahl zwischen 0 und 100 erzeugt, für den 2.Wert eine Zufallszahl zwischen 0 und 100 abzuglich des ersten Wertes usw.
Dazu ein Beispiel:
1. Wert Zufallszahl zwischen 0 und 100 => 40 (Beispielwert)
2. Wert Zufallszahl zwischen 0 und 100-40 also zwischen 0 und 60 => 30 (Beispielwert)
3. Wert Zufallszahl zwischen 0 und 100-40-30 also zwischen 0 und 30 => 10 (Beispielwert)
4. Wert Zufallszahl zwischen 0 und 100-40-30-10 also zwischen 0 und 20 => 15 (Beispielwert)
5. Wert 100 – Wert 1 – Wert 2 – Wert 3 – Wert 4 also 100-40-30-10-15 => 5 (Beispielwert)
Die Verteilung sieht dann aus wie folgt:
< Diagramm Verteilung Variante 2>
Zwar ist die Häufigkeit umso größer, je kleiner der Wert, doch sind Werte aus allen Bereichen vetreten.
Dies gilt jedoch für alle 5 Werte zusammengenommen. Die einzelnen Werte finden sich in folgenden Bereichen:
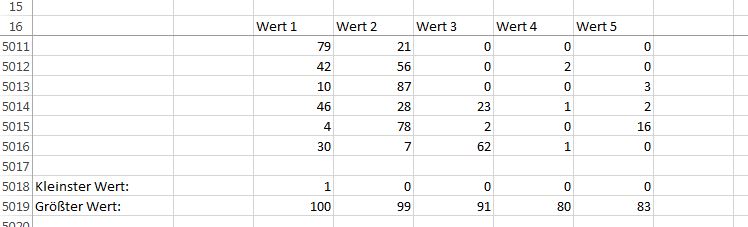 Der erste Wert kann 100 werden, doch für die Folgewerte liegen die größten Wert immer tiefer.
Der erste Wert kann 100 werden, doch für die Folgewerte liegen die größten Wert immer tiefer.
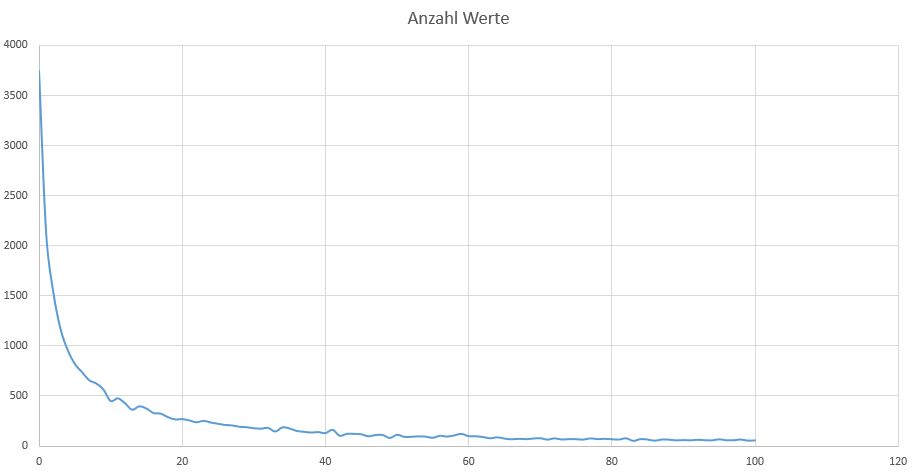
Deutlich verbessern lässt sich das Ergebnis, wenn bei der Generierung der Zufallszahlen nach einem Fünftel der ermittelten Zufallsszahlen rotiert wird. D.h. bei 5.000 Zufallszahlen werden die ersten Tausend Zufallszahlen wie oben beschrieben erzeugt. Bei den zweiten Tausend Zufallszahlen wird für Wert 2 eine Zufallszahl zwischen 0 und 100 erzeugt, für die Werte 2 bis 4 Zufallszahlen innerhalb der verbleibenden Wertebereiche. Wert 1 ergibt sich durch die verbleibende Differenz zu 100. Bei den dritten Tausen Zufallszahlen wird die Zufallszahl zwischen 0 und 100 für Wert 3 erzeugt usw.
Die Gesamtanzahl der Werte verteilt sich dabei in etwa wie im Diagramm Verteilung Variante 2, doch die Zahlenbereiche für die einzelnen Werte sehen wie folgt aus:
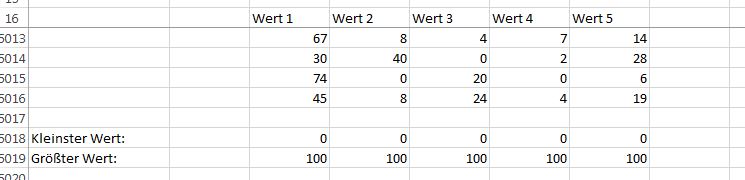 Alle fünf Werte erzeugen Zufallszahlen zwischen 0 und 100. Mit dieser Variante kann die Monte-Carlo-Simulation umgesetzt werden.
Alle fünf Werte erzeugen Zufallszahlen zwischen 0 und 100. Mit dieser Variante kann die Monte-Carlo-Simulation umgesetzt werden.
Die Zufallszahlen für jede Aktie werden in den Spalten B bis F berechnet:
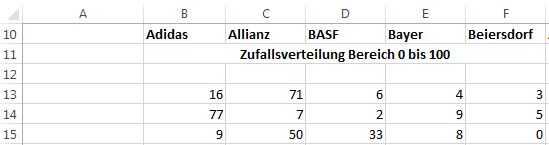 Die Simulation soll mit 10.000 Werten durchgeführt werden. Wie zuvor erwähnt, werden die Zufallszahlen für die ersten 2.000 Wert wie folgt ermittelt:
Die Simulation soll mit 10.000 Werten durchgeführt werden. Wie zuvor erwähnt, werden die Zufallszahlen für die ersten 2.000 Wert wie folgt ermittelt:
 Für die Werte von 2001 bis 4.000 gilt:
Für die Werte von 2001 bis 4.000 gilt:
 Für die Werte von 4001 bis 6.000 gilt:
Für die Werte von 4001 bis 6.000 gilt:
 Für die Werte von 6001 bis 8.000 gilt:
Für die Werte von 6001 bis 8.000 gilt:
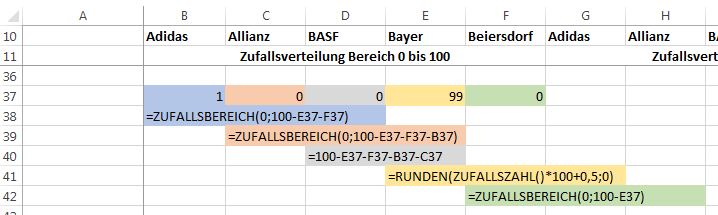 Für die Werte von 8001 bis 10.000 gilt:
Für die Werte von 8001 bis 10.000 gilt:
 Die Zufallszahlen liegen zwischen 0 und 100 (Prozent), da die Funktion “Zufallsbereich” die Verwendung ganzer Zahlen erforderlich macht. In Anlehnung an die früheren Artikel, in denen die Zahlen zwischen 0 und 1 lagen, werden die ermittelten Zufallszahlen in den Spalten G bis K durch 100 dividiert.
Die Zufallszahlen liegen zwischen 0 und 100 (Prozent), da die Funktion “Zufallsbereich” die Verwendung ganzer Zahlen erforderlich macht. In Anlehnung an die früheren Artikel, in denen die Zahlen zwischen 0 und 1 lagen, werden die ermittelten Zufallszahlen in den Spalten G bis K durch 100 dividiert.
 Schritt 8: Tägliche Rendite berechnen
Schritt 8: Tägliche Rendite berechnen
Im Beitrag “Portfolio-Berechnungen mit OpenOffice Calc” wurde die tägliche Rendite des Portfolios wie folgt berechnet:
E(rp) = wT * μ
wT steht für die Gewichtung w transponiert
μ steht für die tägliche Rendite aller Einzelwerte
In diesem Beispiel waren die einzelnen Gewichtungen in einer Spalte untereinander angeordnet. Bei der aktuellen Berechnung sind die Gewichtungen in einer Zeile nebeneinander angeordnet. Somit muss die Gewichtung nicht mehr transponiert werden und die Formel lautet nun:
E(rp) = w * μ
In der Praxis lautet die Formel somit =MMULT((G13:K13);mue) und muss mit “<Strg>+<Shift>+<ENTER>” abgeschlossen werden.
 Schritt 9: Tägliche Varianz und Standardabweichung berechnen
Schritt 9: Tägliche Varianz und Standardabweichung berechnen
Im oben erwähnten Beitrag wurde die tägliche Varianz wie folgt berechnet:
Var = wT * S * w
wT steht für die Gewichtung w transponiert
w steht für die Gewichtung
S steht für die Varianz-Kovarianz-Matrix wie unter Schritt 6 beschrieben
Da die Gewichtungen hier in einer Zeile angeordnet sind, wurde die Formel entsprechend angepasst:
Var = w * S * wT , wobei beide Formeln zum selben Ergebnis führen.
In der Praxis lautet die Formel somit =MMULT(MMULT((G13:K13);_S);MTRANS(G13:K13)) und muss mit “<Strg>+<Shift>+<ENTER>” abgeschlossen werden.
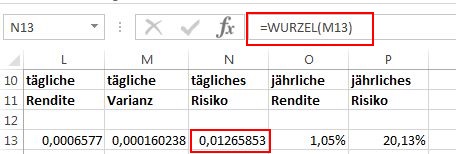
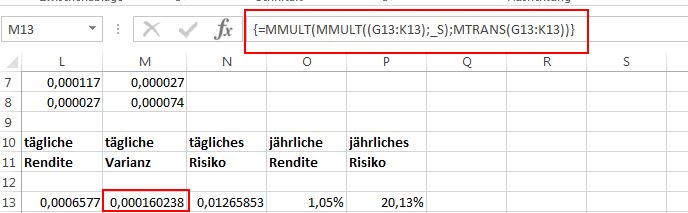 Die Standardabweichung (in der Finanzmathematik häufig als Volatilität bezeichnet und als Maß des Risikos verwendet) berechnet sch aus der Wurzel der Varianz:
Die Standardabweichung (in der Finanzmathematik häufig als Volatilität bezeichnet und als Maß des Risikos verwendet) berechnet sch aus der Wurzel der Varianz:
 Schritt 10: Rendite und Standardabweichung auf Jahresbasis hochrechnen
Schritt 10: Rendite und Standardabweichung auf Jahresbasis hochrechnen
Bisher wurde mit Werten auf täglicher Basis gerechnet. Da die Werte auf Jahresbasis aber wesentlich eingänglicher sind, erfolgt noch die entsprechende Umrechnung.
Dazu sind die täglichen Ergebnisse der Rendite mit der Anzahl der Tage multipliziert werden. Die Anzahl der Tage wurde bereits in Schritt 6 ermittelt (M-1 = 253).
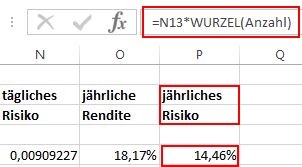
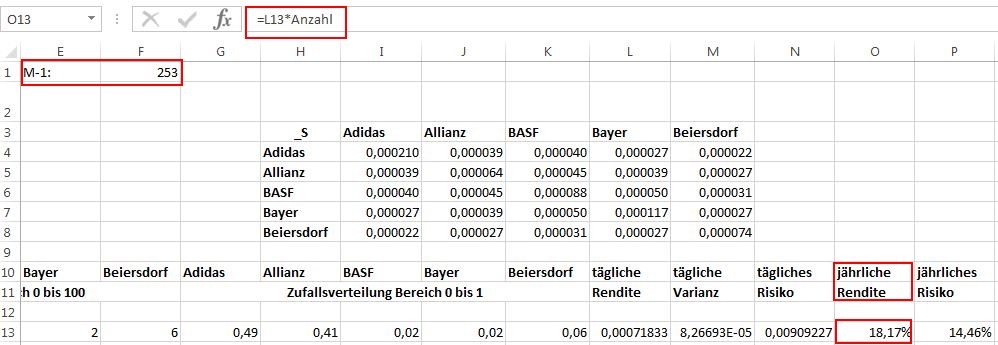 Bei der Standardabweichung (Volatilität, bzw. Risiko) als Ableger der Varianz müssen die tägliche Ergebnisse mit der Wurzel der Anzahl der Tage multipliziert werden..
Bei der Standardabweichung (Volatilität, bzw. Risiko) als Ableger der Varianz müssen die tägliche Ergebnisse mit der Wurzel der Anzahl der Tage multipliziert werden..
 Schritt 10: Auswertung
Schritt 10: Auswertung
Die Auswertung bezieht sich auf das Minimum-Varianz-Portfolio, also ausgelegt auf das minimale Risiko.
Dazu wird zuerst als Hilfswert noch die Zeilennummer mit aufgeführt:
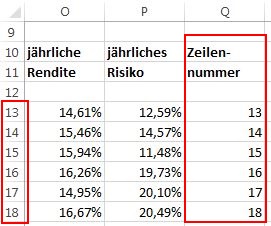 In Folge werden folgende Werte ermittelt:
In Folge werden folgende Werte ermittelt:
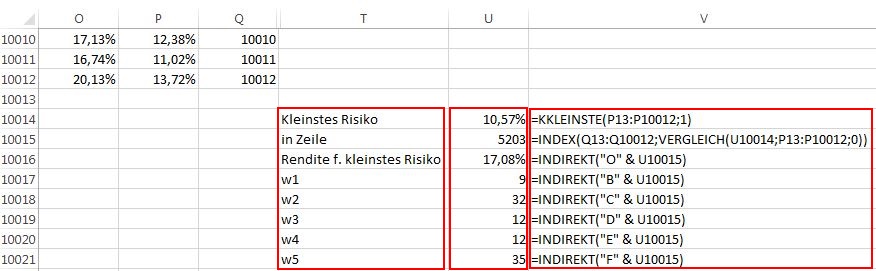 Zuerst wird das kleinste jährliche Risiko aus allen Daten ermittelt. Mit Hilfe der Bestimmung der Zeile, in der das kleinste Risiko auftritt, kann die zugehörige jährliche Rendite und die zugehörigen Gewichtungen der Einzeltitel dargestellt werden.
Zuerst wird das kleinste jährliche Risiko aus allen Daten ermittelt. Mit Hilfe der Bestimmung der Zeile, in der das kleinste Risiko auftritt, kann die zugehörige jährliche Rendite und die zugehörigen Gewichtungen der Einzeltitel dargestellt werden.
Bei der Auswertung müssen wir immer im Auge behalten, dass 10.000 Zufallswerte nicht sehr viel sind, zumal mit dem System keine gleichmäßige Verteilung der Zufallszahlen erfolgt. Mit VisualBasic for Applications (VBA) lassen sich deutlich bessere Lösungen umsetzen.
Dennoch ergeben sich auch für die einfache Umsetzung aussagekräftige Ergebnisse, die sich weiter verbessern lassen, indem mittels der “F9”-Taste neue Zufallszahlen generiert und die einzelnen Ergebnisse festgehalten werden.
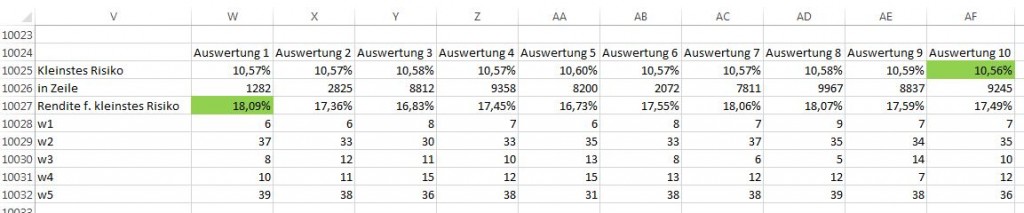 Es ist zu erkennen, dass sich die Resultate für das kleinste Risiko zwischen 10,56 und 10,60% bewegen. Die zugehörigen Renditen liegen im Bereich zwischen
Es ist zu erkennen, dass sich die Resultate für das kleinste Risiko zwischen 10,56 und 10,60% bewegen. Die zugehörigen Renditen liegen im Bereich zwischen 13,73 16,73 und 18,09%. Für Beiersdorf (w5) und Allianz (w2) sind die Gewichtungen mit deutlich über 30% am Höchsten.
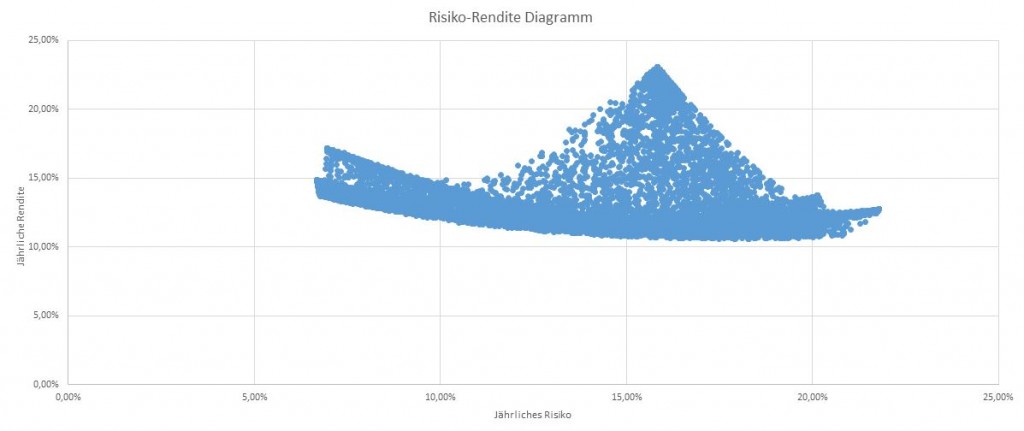
Das Risiko-Rendite Diagramm dazu sieht wie folgt aus:


8 Kommentare
Zum Kommentar-Formular springen
Hallo Mathias,
sehr eindrucksvoll Deine Darstellung der Portfoliooptimierung mi der Monte-Carlo Simulation.
Zunächst sind mir ein paar kleine textliche Druckfehler aufgefallen, die ich nur wegen der besseren Nachvollziehbarkeit kurz aufführen möchte:
Im Schritt 4 steht bei der Überschrift für (Return-Rendite) monatlche Rendite auf Mittelwert, müsste tägliche Rendite auf Mittelwert heißen.
ebenfalls dann unter (A) ebenfalls tägliche Rendite
Im Schritt 10: Auswertung oberhalb des Risiko-Rendite Diagramms wird die Rendite mit 13,73 % angegeben, richtig lt, Tabelle wäre 16,73%
Ich habe mir diese Portfoliooptimierung für meine Zwecke nachgebaut. Ich investiere weltweit in Fonds und habe dadurch sehr schöne Ergebnisse erzielt. Das für mich beste Ergebnis erzielt ich mit der Mischung aus zwei Länderfonds und drei Branchenfonds. Allerdings stellen sich mir folgende Fragen, die Du mir vielleicht beantworten kannst:
1. Der zeitliche Horizont für die Auswahl des geringsten Risikos und der bestmöglichen Rendite ist hier auf ein Jahr festgelegt. Ist das ein ein aussagefähiger Zeitraum, wenn man sein Depot nur monatlich oder später anpassen möchte. Ich habe festgestellt, dass sich die Gewichtungen schon von einem Monat zum nächsten erheblich verändern können oder sollte man das Ergebnis erst nach einem Jahr wieder überprüfen und anpassen?
2. Ich habe die Vorauswahl bei meinen Fonds aufgrund von Erfahrungen der Korrelation und Volatiltität der Fonds getroffen. Gibt es dafür oder ein Programm, dass Fonds auch nach RSI oder VaR Faktoren auswertet? Ansonsten ist es doch sehr mühsam und zeitaufwendig jeden Monat neue mögliche Konstellationen von Fonds durchzuprüfen.
Ich hoffe ich habe mich verständlich ausgedrückt und freue mich über eine Antwort!
Sonnige Grüße
Johann
Autor
Hallo Johann,
vorab vielen Dank für die Hinweise auf die Fehler, die inzwischen korrigiert sind.
Es ist sehr erfreulich zu sehen, dass es Interessenten gibt, die sich so tief mit der Materie befassen.
Der Fehler mit den monatlichen Renditen hat sich dadurch ergeben, dass meine Vorlage zum Artikel auf monatlichen Renditen beruhte, womit wir bei Deiner ersten Frage wären:
Der Zeitraum von einem Jahr und die Verwendung von Tagesschlusskursen wurden nur eingesetzt, um die Vorgehensweise aufzuzeigen.
Da davon auszugehen ist, dass ein optimiertes Portfolio nur erstellt wird, wenn ein längerer Anlagehorizont vorliegt (warum sollte sich jemand die Mühe machen, wenn er nur für ein Jahr investieren will?), macht sicher ein längerer Überprüfungszeitraum Sinn. Konkrete Angaben hierzu sind dünn gesät. Vorschläge zielen auf einen Zeitraum zwischen 3 und 10 Jahren, was dann auch die Verwendung von Wochen-, bzw. Monatsschlusskursen ermöglicht.
Eine monatliche Überprüfung halte ich persönlich für überzogen. Vor allem auch mit dem Hintergrund, dass eine Verbesserung der Rendite um 1% unter Umständen geringer ist als die Kosten für die Umschichtung. Von dem persönlichen Aufwand einmal abgesehen.
Aber auch hier kenne ich keine konkreten Auswertungen, die einen Aktualisierungszeitraum empfehlen können. Persönlich halte ich eine Anpassung einmal jährlich für ausreichend. Sollten größere Verwerfungen an den Börsen auftreten, sollte schon mal auch zwischendurch eine Überprüfung erfolgen.
Die Antwort auf Frage 2 würde ich gerne auf das Wochenende verschieben, da mir aus dem Stegreif nichts bekannt ist. Sollte ich dazu etwas finden, werde ich mich melden.
Beste Grüße
Mathias
Hallo Herr Mathias,
vielen Dank für den interessanten Artikel über die Portfolio-Optimierung mittels Monte-Carlo-Simulation.
Deinen Beitrag nehme ich als Grundlage für eine Umsetzung in einer VB-Programmierung, um so eine Anwendung zu realisieren, die eine flexible Anzahl von Einzelposten erlaubt und Simulations-Durchläufe >= 1000000 ermöglicht.
Meine Portfolio-Daten liegen in einer Access-DB, die ich per SQL-Abfragen entsprechend in Variablen einlese und dann für die Berechnungen heranziehe.
Einschließlich Punkt 4 Deiner Ausführungen kann ich ohne Probleme in VB-Code umwandeln. Auch ist das Erzeugen der unterschiedlichen Zufallszahlen via Select Case in VB relativ einfach zu realisieren.
Da ich mit Matrix-Algebra leider nicht sonderlich vertraut bin, habe ich jedoch Schwierigkeiten mit der Umsetzung der Varianz-Kovarianz-Matrix (Schritt 6 der Anleitung) sowie den Schritten 8 und 9, welche Du mit den Excel-Funktionen MMULT und MTRANS umgesetzt hast. Du hast zwar die Formeln bei den jeweiligen Berechnungen dargelegt, allerdings stoße ich beim “transponieren” an meine Grenzen.
Könntest Du mir vielleicht einen Tipp geben, wie ich die beiden genannten Excel-Funktionen in Visual-Basic übersetzen kann.
Vielen Dank für Deine Rückmeldung und schöne Grüße aus Karlsruhe!
Klaus
Autor
Hallo Klaus,
langsam werde ich eingekreist. Neulich hatte ich Kontakt mit einem Anleger aus Heidelberg, nun kommt Karlsruhe hinzu.
Mein Wohnort liegt so ziemlich genau dazwischen.
Aber Spaß beiseite. Deinen Ansatz mit SQL-Zugriff und VB halte ich für sehr interessant, da sich größere Simulationen mit Excel allein kaum umsetzen lassen.
Der Ansatz ist nicht nur interessant, sondern auch anspruchsvoll.
Persönlich habe ich mir noch keine Gedanken über die Umsetzung der Matrix-Funktionen in eine Programmiersprache. Aber möglicherweise können Dir diese beiden Youtube-Videos weiterhelfen:
“Matrix transpose in vb.net” sowie
“Matrix multiplication in vb.net”
Bitte melden, falls weitere Fragen vorhanden sind. Und viel Erfolg bei der Umsetzung.
Beste Grüße
Mathias
Hallo Mathias,
bevor ich mit Schritt 10 anfangen kann müssen die ganzen Daten vorhanden sein.
Also Zelle auswählen und am rechten unteren Eck der Zelle mit der Maus nach unten ziehen.
Jetzt frage ich mich wie ich eine Matrixformel bspw. bei “tägliche Varianz” für die anderen Zellen von M13:M10000
ziehen kann, sodass die Matrixformel mit den richtigen Faktoren funktioniert.
Derzeit dupliziert open office calc die gleiche Berechnung der Matrix in die anderen Felder M13:M10000.
Bsp.: MMULT(MMULT((G13:K13);_S);MTRANS(G13:K13))
dort kann ich jetzt händisch für die nächste Zeile G14:K14 etc. eintragen, aber wie kann ich das automatisch machen? Mit $ Zeichen? Wenn ja wo kommen diese hin?
Vielen Dank für Ihre Hilfe
Freundliche Grüße
Sascha
Autor
Hallo Sascha,
ich habe die Simulation mit Excel umgesetzt. Hier funktioniert alles problemlos.
In OpenOffice Calc muss ich die Simulation erst noch umsetzen. Ich habe eine kleine Beispielberechnung erstellt,
hier funktioniert auch alles. Könntest Du mir Deine Calc-Datei zukommen lassen?
Beste Grüße
Mathias
Die Efficient Frontier in diesem Beispiel sieht sehr “merkwürdig” aus. Ich kenne das als Parabolle, bzw. Parabollenform
Siehe dazu:
https://en.wikipedia.org/wiki/Efficient_frontier
Liegt das am 5er Portfolio? In meinem Beispiel mit 3 Assets ist es eine Parabolle geworden, wie ich sie kenne.
Autor
Wenn die Zufallsverteilung der einzelnen Aktien wirklich einigermaßen gleich verteilt wäre, so sollte eine Parabelform in der grafischen Übersicht zu sehen sein.
Meist ist aber eine Aktie mit einem hohen Anteil versehen, während die restlichen Aktien nur den Rest aufteilen.
Deshalb die Beschreibung im Text, wie ich versucht habe, dies abzumildern. Beseitigen konnte ich es aber nicht.
Aber bei der Monte-Carlo-Methode spielt dies eine untergeordnete Rolle, solange die Anzahl der Simulationsdurchläufe groß genug ist.
Ziel ist nicht die Ausgabe der Grafik, sondern die Zusammensetzung des Depots. Die Aussage steckt also in der Tabelle über der Grafik:
Das beste Chance-Risiko-Verhältnis ergibt sich bei folgendem Bereich der einzelnen Aktien:
Aktie 1: 6% bis 9% Mittelwert: 7,1%
Aktie 2: 30% bis 37% Mittelwert: 34,2%
Aktie 3: 5% bis 14% Mittelwert: 9,7%
Aktie 4: 7% bis 15% Mittelwert: 11,9%
Aktie 5: 31% bis 39% Mittelwert: 37,1%
Falls Punkte unvollständig oder nicht nachvollziehbar sind, bitte nachhaken.