Einführung in die Monte-Carlo-Simulation

Die Monte-Carlo-Simulation (auch als Monte-Carlo-Methode bezeichnet) ist ein Verfahren aus der Statistik und Wahrscheinlichkeitsrechnung.
Dabei werden sehr häufige Zufallsexperimente durchgeführt, die als Basis für die numerische Lösung eines Problems dienen.

Der Ursprung der Monte-Carlo-Simulation geht bis in das 18.Jahrhundert zurück. Die Weiterentwicklung erfolgte im Rahmen des Baus der Atombombe in Los Alamos. Dabei wurde für das Verfahren der Codename “Monte Carlo” angeblich in Anspielung auf die Spielbank von Monte Carlo vergeben.

Die Monte-Carlo-Methode kommt in vielen Bereichen zur Anwendung, beispielsweise in der Mathematik, Physik, Chemie und der Finanzbranche.

Da das Verfahren aus der textlichen Beschreibung heraus schwer nachzuvollziehbar ist, wollen wir im weiteren Verlauf ein Beispiel für die Monte-Carlo-Simulation durchspielen.

Grundlagen der Berechnung von Pi mit der Monte-Carlo-Simulation

Zu Beginn muss ein mathematisches Modell erstellt werden. Für das Beispiel kommt die Formel zur Berechnung der Kreisfläche zum Einsatz:

Dabei gilt:

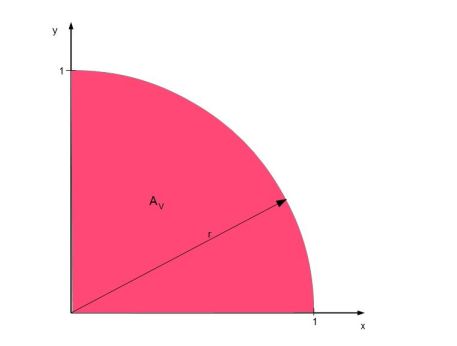
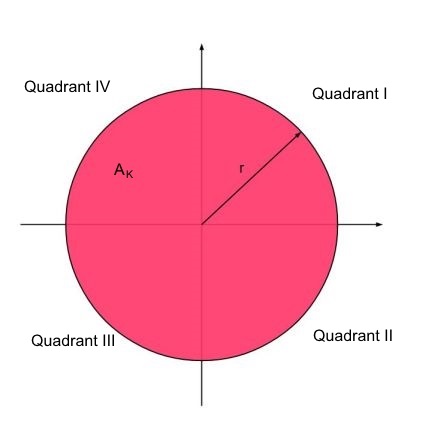
Grafisch sieht das Ganze dann wie folgt aus:

Da Pi ermittelt Werden soll, wird die Formel entsprechend umgestellt:

Wie im oberen Bild zu sehen ist, erstreckt sich die Kreisfläche über alle 4 Quadranten, d.h. mit x- und y-Werten zwischen -1 und 1. Die Arbeit kann erleichtert werden, indem nur der 1.Quadrant zur Auswertung verwendet wird.

wobei gilt

Wie leicht nachzuvollziehen ist, entspricht die Fläche von 4 Viertelkreise der Fläche des ganzen Kreises. Das wird in obige Formel eingesetzt und ergibt somit

Im nächsten Bild sind zufällig 10 Punkte (gekennzeichnet durch ein “x”) verteilt.

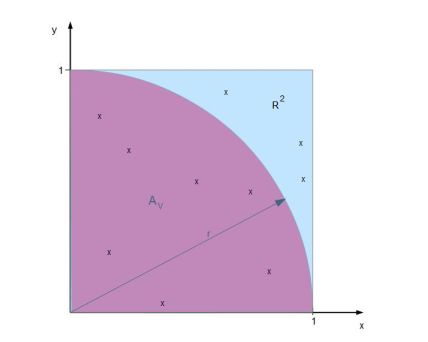Im Kreisauschnitt (A_V) befinden sich 7 Punkte und im gesamten Quadrat (R²) 10 Punkte. Werden die Resultate in die Formel eingesetzt, ergibt sich

Das Ergebnis ist ziemlich weit vom tatsächlichen Wert entfernt. Allerdings wurden nur sehr wenige Zufallswerte verwendet. Je mehr Punkte zufällig angeordnet werden, desto genauer wird das Ergebnis. Wie das mit einem Tabellenkalkulationsprogramm umgesetzt wird, soll im nächsten Abschnitt behandelt werden.

Berechnung von Pi mit der Monte-Carlo-Simulation in Excel

Die folgenden Berechnungen wurden in Excel durchgeführt, laufen aber z.B. mit OpenOffice Calc identisch ab.

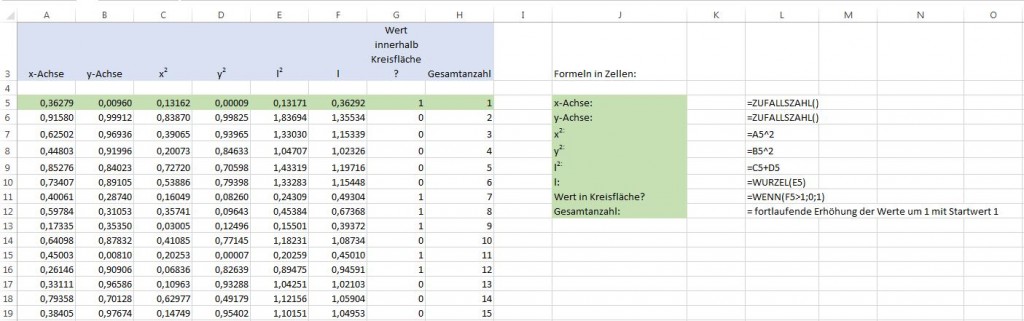<Durch einen Klick auf das Bild kann es im Vollbildmodus geöffnet werden>

Der Radius r soll 1 betragen. Deshalb werden in den Spalten A und B Zufallszahlen für die x- und y-Werte zwischen 0 und 1 erzeugt. Der Abstand l vom Nullpunkt wird durch den Satz des Phythagoras bestimmt:

Die jeweiligen Werte werden in den Spalten C bis F berechnet.
Ob der Abstand l innerhalb oder außerhalb der Kreisfläche liegt, wird in Spalte G ermittelt. Ist der Abstand größer als der Radius 1, so liegt der Wert außerhalb, ansonsten innerhalb der Kreisfläche. In Spalte H wird einfach die Anzahl der Versuche hochgezählt.
Ein Beispiel für die Auswertung ist im nachfolgenden Screenshot zu sehen:

<Durch einen Klick auf das Bild kann es im Vollbildmodus geöffnet werden>

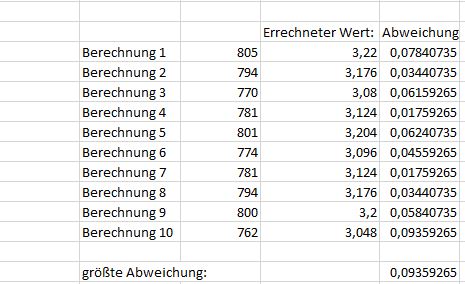
Im Beispiel mit 100 Zufallswerten wurde ein Wert für Pi von 3,04 ermittelt. Die große Abweichung lässt deutlich erkennen, dass 100 Versuche zu wenig sind. Die Aussagekraft der Ergebnisse lässt sich noch besser darstellen, indem mehrere Werte hintereinander ermittelt werden und die größte Abweichung festgestellt wird.

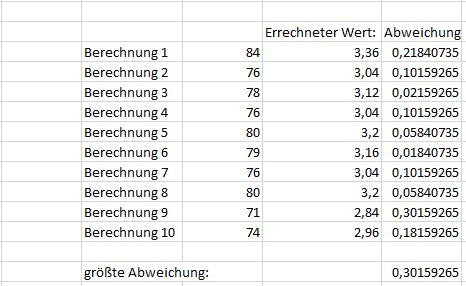 In den 10 Überprüfungen mit 100 Zufallspunkten beträgt die größte Abweichung rund 0,3.
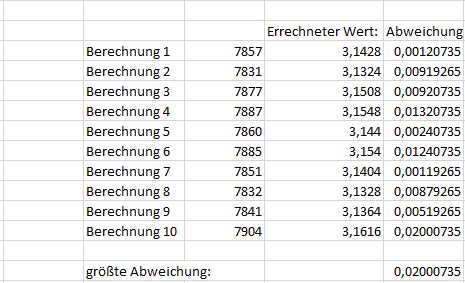
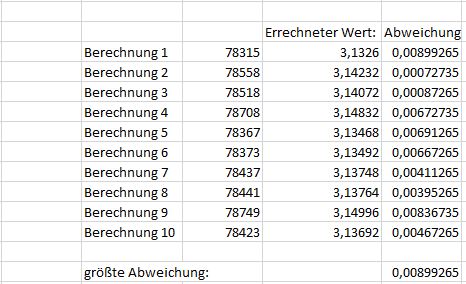
Die gleiche Vorgehensweise übernehmen wir nun für 1.000, 10.000 und 100.000 Versuche:

1.000 Versuche

10.000 Versuche

100.000 Versuche

Wie zu erkennen ist, wird die Abweichung zum tatsächlichen Wert mit steigender Anzahl von Zufallsversuchen immer geringer.
Mit diesen Grundlagen wollen wir das Monte-Carlo-Verfahren in den beiden folgenden Artikeln themenbezogen einsetzen. Zuerst kommt die Methode zur Portfoliooptimierung zum Einsatz, danach soll die zukünftige Kursentwicklung von Aktien abgeschätzt werden.