Der exponentiell gleitende Durchschnitt (exponential moving average – EMA) zählt ebenfalls zu den Trendfolgeindikatoren.
Im Vergleich zum einfachen gleitenden Durchschnitt werden den aktuelleren Kursen eine höhere Gewichtung beigemessen.
Die Formel für den exponentiell gleitenden Durchschnitt (EMA) lautet:
EMAt = (ct – EMAt-1) * SF + EMAt-1
Selbstverständlich müssen Sie die Formel weder kennen noch verstehen, da der EMA in den meisten Charts als Indikator ausgewählt werden kann. Für den interessierten Leser wollen wir die Berechnung hier dennoch erläutern.
- EMAt ist der berechnete exponentiell gleitende Durchschnitt zum aktuellen Zeitpunkt.
- EMAt-1 ist der berechnete exponentiell gleitende Durchschnitt von der vorausgehenden Periode (üblicherweise vom Vortag).
- ct ist der Schlußkurs der verwendeten Periode – meist der Tagesschlußkurs.
- SF (smoothing factor) ist der Glättungsfaktor, der mit 2 / (n + 1) berechnet wird. Dabei entspricht “n” der Berechnungsperiode, d.h. bei einem 9-Tage-EMA wäre n = 2 / (9 + 1) = 0,2.
Zur praktischen Umsetzung wollen wir wieder Wolfgang’s Korbproduktion aus dem Beitrag über den einfachen gleitenden Durchschnitt verwenden:
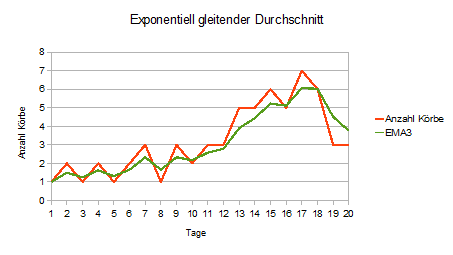Zuerst setzen wir den 3-Tage-EMA ein. Am ersten Tag des Betrachtungszeitraumes entspricht der EMA immer dem Startwert. In unserem Beispiel also die “1”, da am ersten Tag 1 Korb produziert wurde.
Nun setzen wir die Werte für Tag 2 in die Formel ein:
- ct = 2 (am 2.Tag wurden 2 Körbe produziert)
- EMAt-1 = 1 (berechneter Wert von Tag 1)
- n = 3 (3-Tage EMA) => SF = 2 / (3 + 1) = 0,5
EMA2 = (2 – 1) * 0,5 + 1 = 1,5
Für den 3.Tag erhalten wir folgende Werte:
- ct = 1 (am 3.Tag wurde 1 Korb produziert)
- EMAt-1 = 1,5 (berechneter Wert von Tag 2)
- SF = 0,5 (s.o. – der Glättungsfaktor ist für den gesamten Zeitraum konstant)
EMA3 = (1 – 1,5) * 0,5 + 1,5 = 1,25
Für den 4.Tag erhalten wir folgende Werte:
- ct = 2 (am 4.Tag wurden 2 Körbe produziert)
- EMAt-1 = 1,25 (berechneter Wert von Tag 3)
- SF = 0,5 (s.o. – der Glättungsfaktor ist für den gesamten Zeitraum konstant)
EMA4 = (2 – 1,25) * 0,5 + 1,25 = 1,625
Und so geht es weiter bis zu Tag 20. Mit einem Tabellenkalkulationsprogramm wie Excel oder OpenOffice Calc lassen sich die Berechnungen bei Bedarf einfach umsetzen.
Werfen wir noch einen Blick auf den 6-Tage EMA:
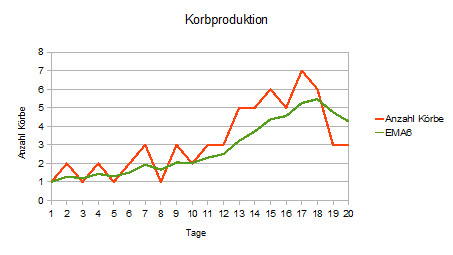Es ist der gleiche Zusammenhang erkennbar wie beim einfach gleitenden Durchschnitt: je länger der Zeitraum wird, in dem die Werte einer Periode zusammengefasst wird, desto mehr wird die Kurve geglättet.
Erkennbar ist dies auch am Glättungsfaktor. Dieser betrug beim 3-Tage-EMA 0,5. Beim 6-Tage-EMA erhalten wir: SF = 2 / (n + 1) = 2 / (6 + 1) = 0,2857.
Zum Abschluß wollen wir noch den 6-Tage-EMA und den 6-Tage-SMA (einfach gleitender Durchschnitt) gegenüberstellen:
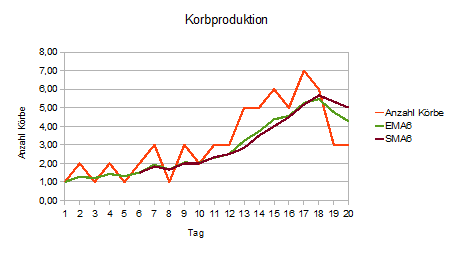Zwei Unterschiede fallen sofort ins Auge:
- Beim einfach gleitenden Durchschnitt erhalten wir den ersten Wert nach 6 Tagen, beim exponentiell gleitenden Durchschnitt steht der erste Wert bereit nach dem ersten Tag zur Verfügung.
- Der exponentiell gleitende Durchschnitt reagiert schneller auf größere Ausschläge des Basiswertes.
Somit wird der EMA gerne von Investoren eingesetzt, die schnell auf Trendwechsel reagieren wollen. Doch auch diese Münze hat zwei Seiten: durch die schnellere Reaktionszeit steigt die Gefahr von Fehlsignalen.
Weitere Beiträge zu dieser Thematik:
2 Pings
[…] « Exponentiell gleitender Durchschnitt […]
[…] Exponentiell gleitender Durchschnitt » […]