Monte-Carlo-Simulation von Aktienkursen Teil 2

Im ersten Teil zur Simulation von Aktienkursen mit der Monte-Carlo Methode wurde eine einzelne, zufällige Kursbewegung erstellt.
Doch das Prinzip der Monte-Carlo-Simulation besteht nicht aus der Berechnung eines einzelnen Ergebnisses, sondern aus der Auswertung einer Vielzahl von zufälligen Ergebnissen.
Wer also den genauer Kurs einer Aktie in einem Jahr wissen will, sollte sich an den Wahrsager seiner Wahl wenden. Wer aber den wahrscheinlichen Kursbereich, in dem sich eine Aktie in einem Jahr bewegen könnte, liegt mit der Monte-Carlo Simulation richtig.

Die Grenzen der Simulation wurden bereits im ersten Teil angesprochen, und ich möchte sie an dieser Stelle wiederholen, damit keine Missverständnisse aufkommen:
Die Resultate beruhen auf historischen Daten. Ändern sich also die Rahmenbedingungen wie das Marktumfeld (z.B. Eintritt in Rezession) oder unternehmensspezifische Kriterien (z.B. Wettbewerb, Herstellungskosten, Produktakzeptanz etc.), wird eine Neubewertung erforderlich.
Zum Ende des Artikels werden wir nochmals auf einige Einsatzmöglichkeiten zurückkommen.

Doch vorab soll in vier weiteren Schritten, die Simulation und deren Auswertung fertiggestellt werden.

Schritt 9 – Kursermittlung zusammenfassen

Bisher mussten zur Kursermittlung drei Spalten verwendet werden. Im weiteren Verlauf soll dies in nur einer Spalte umgesetzt werden. Dazu schauen wir uns den Aufbau an:
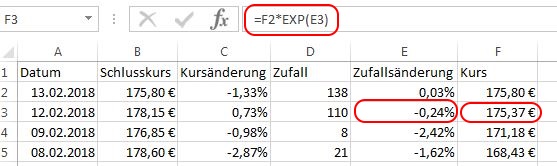Der erste zufällig ermittelten Kurs ist in der Zelle “F3” zu finden, da in “F2” ja der letzte Kurs der historischen Daten als Startwert verwendet werden muss. Für die Kursberechnung wird nun der Startwert (F2) und die Zufallsänderung in Spalte “E” benötigt.
Nun werfen wir einen Blick auf die Spalte “E”:

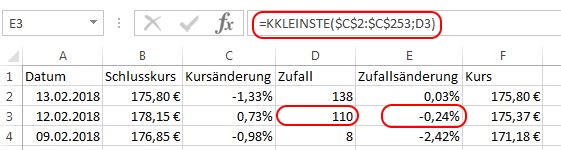Wir wollen nun in Spalte F3 den Wert von E3 durch die Formel in E3, also “KKLEINSTE($C$2:$C$253;D3)” ersetzen, was dann wie folgt aussieht:

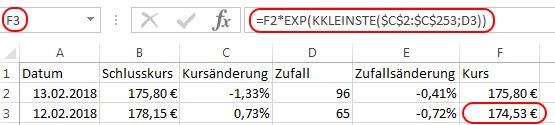Aus Spalte “E” wird nun kein Wert verwendet, womit die Spalte gelöscht werden kann.

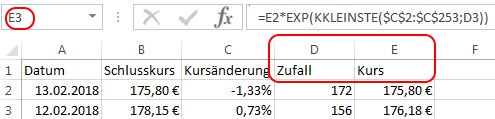Der Kurs steht nun in Spalte “E”. Excel hat – wie alle mir bekannten Tabellenverarbeitungsprogramme – die schöne Eigenschaft, dass die Bezüge auf Spalten nach dem Löschen oder Hinzufügen einer Spalte angepasst werden, solange diese nicht durch die Verwendung des “$”-Zeichens einen festen Bezug erhalten haben. Somit wurde unter “F3 = F2*EXP(…” automatisch “E3 = E2*EXP(…”.

Ab Zelle “E4” erscheint nun aber die Fehlermeldung “#BEZUG!”. Hintergrund ist ganz einfach, dass die Formel ab der Zelle noch nicht angepasst wurde und entsprechend noch nach dem Inhalt der gelöschten Spalte “E” gesucht wird. Das Problem wird im weiteren Verlauf durch Übernahme der Formel zur Kursermittlung auf die weiteren Zellen behoben werden.

Nachdem Spalte “E” eliminiert wurde, erfolgt nur noch der Aufruf des Wertes in Spalte “D”, bezogen auf “E3” der Aufruf von “D3” innerhalb der Formel “KKLEINSTE”.
“D3” beinhaltet folgende Formel:

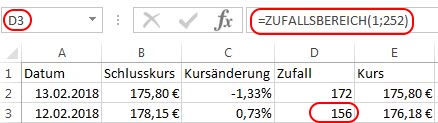Somit müssen wir den Ausdruck “D3” in Spalte “E” lediglich noch durch dessen Inhalt “ZUFALLSBEREICH(1;252)” ersetzen, was dann wie folgt aussieht:

Nun können wir auch Spalte “D” löschen.
Um nun die Bezugsfehler zu beheben, klicken wir auf die Zelle “D3”.

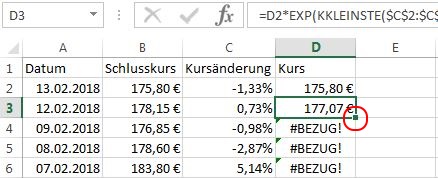Ein kleines, schwarzes Quadrat wird sichtbar. Sobald Sie mit der Maus in den Bereich des Quadrates kommen, erscheint am Cursor ein schwarzes Kreuz. Halten Sie nun die linke Maustaste gedrückt und bewegen Sie den Cursor bis zur letzten Zeile mit der Fehlermeldung. Damit werden die Inhalte kopiert und die Fehlermeldungen verschwinden.

Falls Sie noch das in Teil 1 erstellte Diagramm auf dem Tabellenblatt haben, werden Sie nun einen neuen Chartverlauf sehen. Bei mir sieht er augenblicklich folgendermaßen aus:

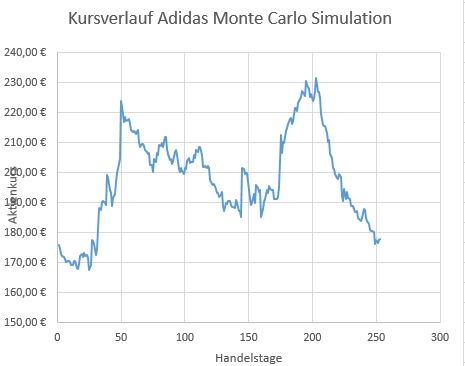Bitte beachten Sie, dass nach jeder Änderung im Tabellendokument neue Zufallszahlen erzeugt werden und somit auch das Diagramm jedesmal angepasst wird. Deshalb sind in den Screenshots oben auch unterschiedliche Werte zu finden, obwohl die selben Zellen angezeigt werden.
Mit der Funktionstaste “F9” können die Zufallszahlen auch ohne Änderungen aktualisiert werden.

Schritt 10 – Viele Zufallskurse anzeigen

Wie bereits mehrfach erwähnt, ist es das Ziel der Monte-Carlo-Simulation, viele zufällige Kurse zu erzeugen. Dazu haben wir nun die Voraussetzungen geschaffen. Es ist lediglich noch ein kleines Problem aus dem Weg zu räumen:

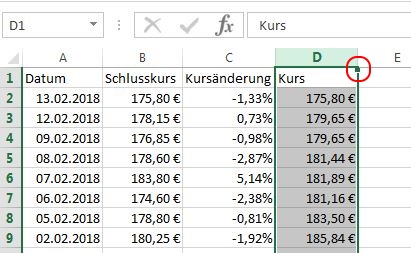Lassen Sie uns Spalte “D” markieren, den Cursor auf das schwarze Quadrat platzieren und gedrückt halten, während wird die Kursdaten auf Spalte “E” kopieren. Unglücklicherweise kann es dabei leicht vorkommen, dass die Spaltenbreite verändert wird, anstatt dass die Spalte kopiert wird. Deshalb empfiehlt es sich, das Quadrat knapp unterhalb der Linie anzuwählen.

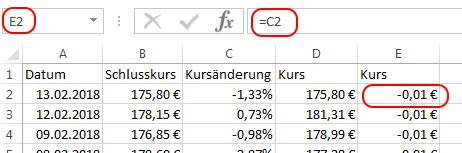Mit den hier verwendeten daten steht nun -0,01 € in Spalte “E”. Ein Blick auf die Formel zeigt, dass wir hier auf die Zelle “C2” zugreifen, statt auf “B2”, wo unsere Schlusskurse zu finden sind. Das Problem lässt sich sehr einfach beheben, indem in Spalte “D2” ein Dollarzeichen vor den Spaltenwert in der Formel gesetzt wird. Also aus “=B2” wird “=$B2”.

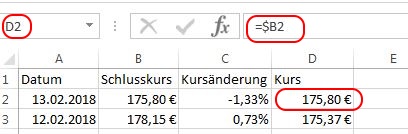Nun kann Spalte “D” viele Male in die nachfolgenden Zeilen – wie beschrieben – kopiert werden.
Der Übersichtlichkeit halber habe ich nur 100 Kursdaten verwendet. In der Praxis werden es deutlich mehr sein.
Hier ein Auszug:

Als Liniendiagramm sieht das ganze dann wie folgt aus:

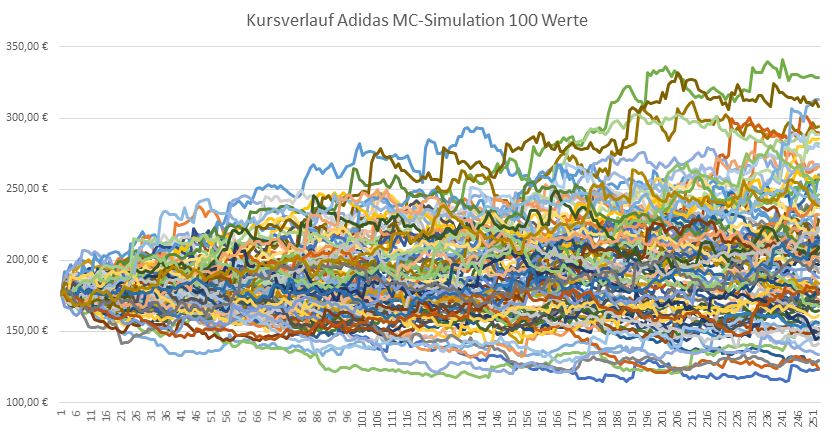Erstellt wurde das Diagramm, indem alle Kursdaten (hier von D2 bis CY254) markiert wurden und anschließend über “Einfügen” – “Diagramm” – “Liniendiagramm” der Typ ausgewählt wurde.

Schritt 11 – Auswertung

Vorab an dieser Stelle nochmals der Hinweis, dass die Verwendung der Monte-Carlo-Simulation nur solange Sinn macht, soweit die unternehmensspezifischen und marktspezifischen Rahmenbedingungen nicht deutlich von denen der historischen Daten abweichen.

Auch lässt sich das Thema Auswertung hier nur stiefmütterlich behandeln, da diese sich letztendlich nach dem Zweck des jeweiligen Benutzers richtet.

Wie weit die historischen Daten zurückreichen sollen und über welchen Zeitraum die Simulation laufen sollte, ist ebenfalls abhängig von der Zielsetzung.
Die Monte-Carlo-Simulation wird z.B. beim Einsatz von Hebelprodukten verwendet, um das Risiko eines Totalverlustes oder eines selbst gewählten Stopp-Loss zu berechnen. Da hier meist kürzer Haltezeiten als beim Kauf von Aktien geplant sind, wird auch der Zeitraum der verwendeten historischen Daten und der Simulation kürzer sein (z.B. 3 Monate, sofern es sich nicht um Daytrading handelt). Im weiteren Verlauf werden wir zu dieser Art der Auswertung ein Beispiel sehen.

Im folgenden werden einige Möglichkeiten der Auswertung vorgestellt:

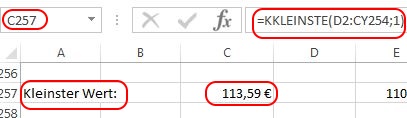Mit der Formel “KKLEINSTE” lässt sich der kleinste Wert aus dem gesamten Wertebereich der Simulation auslesen. In dem speziellen Fall war dies 113,59 €.

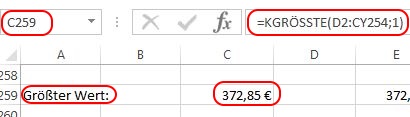Mit der Formel “KGRÖSSTE” lässt sich der größte Wert aus dem gesamten Wertebereich der Simulation auslesen. In dem Fall  372,85 €.

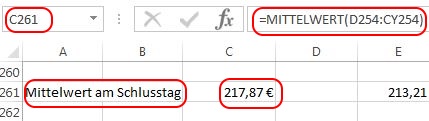Eine weitere Möglichkeit ist die Bildung von Mittelwerten (also Durchschnittskursen) zum Schlusstag. Dies lässt sich selbstverständlich für jeden beliebigen Tag im Beobachtungszeitraum erstellen.
Hier wurde bewusst darauf verzichtet, einen Mittelwert über den gesamten Simulationszeitraum zu erstellen, da zu Beginn die Abweichungen sehr gering sind und damit das Gesamtergebnis nicht repräsentativ ist.

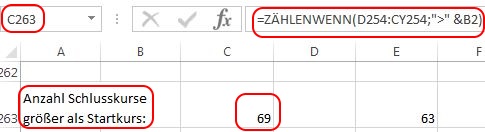Interessant ist die Anzahl der Schlusskurse, die höher notieren als der Startkurs. Umgesetzt wird dies mit der “ZÄHLENWENN”-Funkion. Da die Simulation über 100 Spalten abläuft, entspricht der Wert “69” hier auch dem prozentualen Verhältnis.
Anstelle des Zählkriteriums bezogen auf die Zelle B2 “>” &B2 könnte der Anfangskurs auch direkt in der Form “>175,80” eingetragen werden.

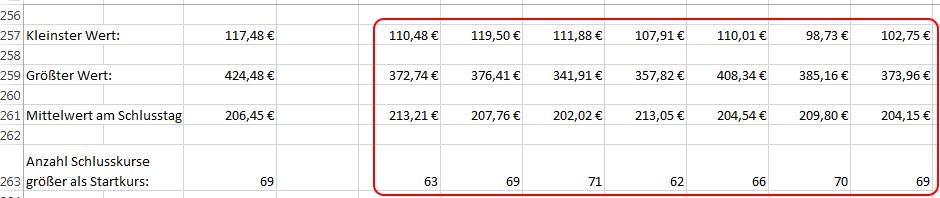Hier werden aufgrund der Übersictlichkeit lediglich 100 Simulationen durchgeführt. In der Praxis sollten mindestens 1000 Simulationen pro Durchlauf erfolgen. Zusätzlich verbessern lässt sich das Ergebnis, wenn erzielte Resultate kopiert und die reinen Werte in weiteren Zellen eingefügt werden, um ein breiteres Ergebnisspektrum vorliegen zu haben.

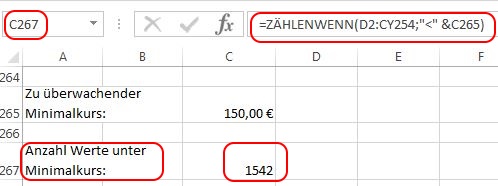Im Vorfeld wurde bereits darauf hingewiesen, dass es sinnvoll sein kann die Anzahl der Kurse unter (oder auch über) einem festgelegten Sollwert auszuwerten. Auch diese Auswertung wird mit der Funktion “ZÄHLENWENN” umgesetzt.
In diesem Simulationslauf waren 1542 Kurse unterhalb des Schwellkurses. Allerdings ist der reine Zahlenwert nicht sehr aussagekräftig.

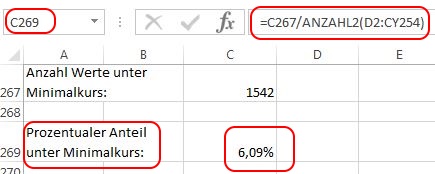Deshalb setzen wir die Anzahl der Kurse unter dem Schwellwert in Bezug zu allen Kursdaten. Da dies auf manuellem Wege sehr mühsam werden kann, verwenden wir hierzu die Funktion “ANZAHL2”, die alle Zellen im Datenbereich zählt, die nicht leer sind, was auf unsere simulierten Daten ja zutrifft.

Soweit die Ausführungen zum Thema Monte-Carlo-Simulation. Über Kritik, Fragen und Anregungen würde ich mich freuen.