Dez. 14

Eine einfache Berechnung des inneren Wertes nach Benjamin Graham

Von Mathias Maier unter Blog, Strategie

Benjamin Graham stellt in seinem Buch „Intelligent investieren“ (bei Amazon bestellen: Intelligent Investieren: Der Bestseller über die richtige Anlagstrategie) eine einfache Formel zur Berechnung des inneren Werts einer Aktie vor.
Werfen wir einen Blick auf die Formel:

Wert einer Aktie = Gewinn pro Aktie * (8,5 + 2 * Wachstum [%])

Zur Berechnung des inneren Wertes werden zwei Angaben benötigt:

– Der „Gewinn pro Aktie“ (häufig auch „Ergebnis pro Aktie“)
– Das Wachstum in Prozent (jährliches Gewinnwachstum)

Wie Sie die Werte ermitteln, wird im weiteren Verlauf vorgestellt.
Lassen Sie uns die Berechnung anhand des virtuellen Unternehmens ABC AG anwenden. Die ABC AG erwirtschaftet einen Gewinn pro Aktie von 3 €. Das jährliche Gewinnwachstum beträgt 4%:

Wert der Aktie = 3,00 € * (8,5 + 2 * 4) = 49,50 €

Was sagt die Formel aus?

Gesetzt der Fall, der Gewinn pro Aktie eines Unternehmens beträgt 1 € und das KGV ist 10, dann ist der Aktienkurs 10 €. Mathematisch wird das Ergebnis ermittelt durch:

Aktienkurs = Gewinn pro Aktie * KGV

Kommt Ihnen der Ausdruck bekannt vor? Die Grahamsche Formel besteht aus den gleichen Bestandteilen. Teil 1 ist der Gewinn pro Aktie, Teil 2 – der Wert in der Klammer – entspricht dem KGV.
Betrachten wir Teil 2 alleine, so können wir feststellen, dass Graham jeder Aktie in Abhängigkeit vom Wachstum ein bestimmtes KGV zugesteht.
Ist das Wachstum Null, so darf das KGV 8,5 betragen. Bei einem Wachstum von 5% ist ein höheres KGV von 18,5 zulässig usw. Somit sind die entscheidenden Parameter das jährliche Gewinnwachstum und das KGV.
Die Berechnung geht also in die ähnliche Richtung wie die Kennzahl „KGV-Wachstums-Verhältnis“ (englisch: PEG – price/earning to growth ratio).

Was ist bei den Angaben zu beachten?

Die jährliche Wachstumsrate soll über einen Zeitraum von 7 bis 10 Jahren errechnet werden.
So einfach die Berechnung durchzuführen ist, so problematisch kann die korrekte Ermittlung der erforderlichen Angaben sein.

Problem 1:

Die nachfolgenden Berechnungen wurden im November/Dezember 2014 erstellt. Welche Werte für den Gewinn pro Aktie (die entsprechend auch in die Festlegung der Wachstumsrate eingehen) sollen verwendet werden? Die Werte der letzten Geschäftsberichte, die in den meisten Fällen aus dem Jahr 2013 stammen, oder die geschätzten Gewinne für 2014, die in vielen Börsenzeitschriften und Finanzportalen zu finden sind.

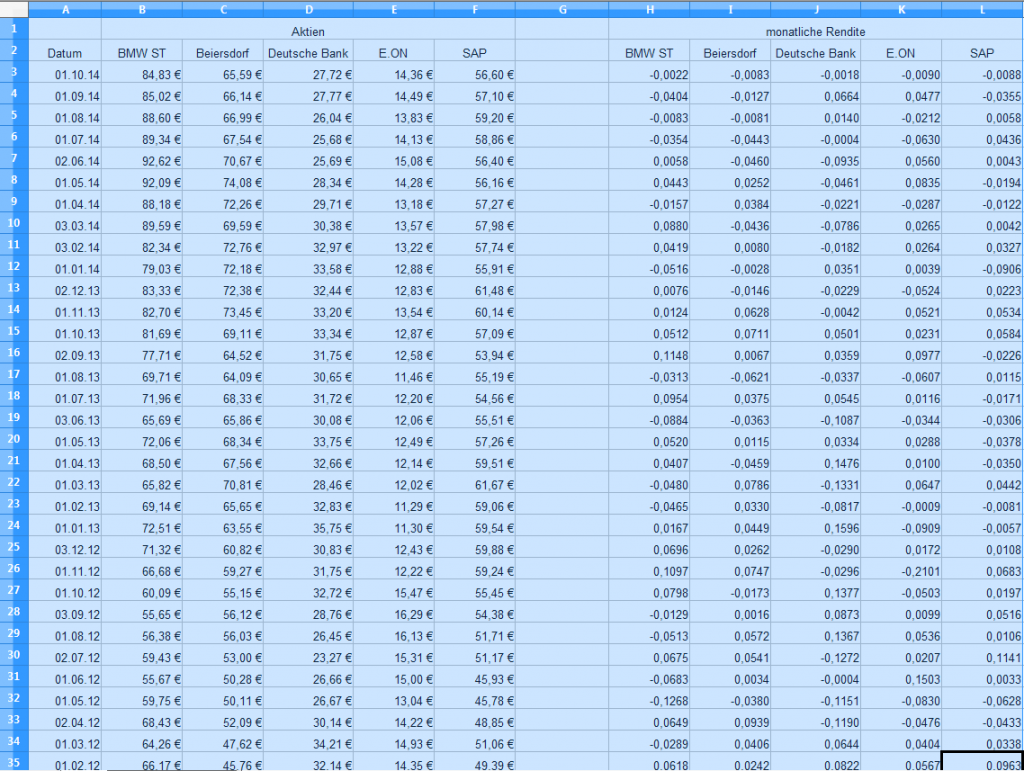
Vergleichen wir die Auswirkungen der Verwendung unterschiedlicher Zeiträume am Beispiel der alphabetisch ersten fünf DAX-Werte.
Im ersten Beispiel wird der Zeitraum von 2004 bis 2013 verwendet, im zweiten Beispiel von 2005 bis 2014.
Die Wachstumsrate wird mittels der jährlichen (annualisierten) Wachstumsrate (englisch: CAGR – Compound Annual Growth Rate) berechnet:

CAGR(t_n,t₀₎ = (Vt_n / Vt₀)^^1/N -1 wobei gilt:

t_n = aktuellstes Jahr ( im ersten Beispiel 2013)
t₀ = Startjahr (im ersten Beispiel 2004)
Vt_n = aktuellste betrachtete Größe ( im ersten Beispiel der Gewinn pro Aktie im Jahr 2013)
Vt₀ = betrachtete Größe des Startjahrs ( im ersten Beispiel der Gewinn pro Aktie im Jahr 2004)
N = Anzahl der Zeiteinheiten t_n – t₀( im ersten Beispiel 2013 – 2004 = 9)

Am Beispiel von Adidas sieht die Kalkulation wie folgt aus:

CAGR(2013, 2004) = (3,76 € / 1,64 €)^^1/9 – 1 = 0,09657 = 9,66%

Beispiel 1

	Gewinn 2013	Gewinn 2004	Wachstum 10 Jahre	innerer Wert
Adidas	3,76 €	1,64 €	9,66%	104,58 €
Allianz	13,05 €	5,98 €	9,06%	347,33 €
BASF	5,27 €	1,72 €	13,25%	184,43 €
Bayer	3,86 €	0,83 €	18,62%	176,58 €
Beiersdorf	2,35 €	1,29 €	6,89%	52,36 €

Beispiel 2

	Gewinn 2014e	Gewinn 2005	Wachstum 10 Jahre	innerer Wert
Adidas	3,10 €	1,93 €	5,41%	59,87 €
Allianz	13,96 €	11,24 €	2,44%	186,71 €
BASF	5,38 €	2,87 €	7,23%	123,54 €
Bayer	4,65 €	2,19 €	8,73%	120,68 €
Beiersdorf	2,37 €	1,45 €	5,61%	46,74 €

Vergleichen wir beide Tabellen, so können wir gravierende Unterschiede feststellen. Lediglich bei Beiersdorf ist der innere Wert annähernd gleich. Bei Adidas und Allianz hingegen sind die inneren Werte mit den Zahlen von 2004 bis 2013 berechnet fast doppelt so groß als beim Zeitraum 2005 bis 2014.

Problem 2:

Unabhängig von den oben festgestellten Unterschiede durch unterschiedliche Zeitreihen ist es in der Regel sinnvoll mit den aktuellsten Daten zu arbeiten – in unserem Fall mit den Gewinnen von 2014.
Wie bereits erwähnt sind die offiziellen Zahlen für 2014 üblicherweise erst im Laufe des Jahres 2015 verfügbar. Somit müssen Gewinnschätzungen verwendet werden. Schätzungen haben es nun an sich, dass sie nicht genau, sondern Näherungen sind. Zudem weichen die Prognosen je nach Quelle voneinander ab. Bei großen, häufig überprüften Unternehmen wie z.B. den DAX-Werten liegen die Abweichungen meist noch in einem begrenzten Rahmen, doch bei kleineren Werten können große Abweichungen zu finden sein.

Problem 3:

Sobald einer der beiden Gewinnangaben, also entweder der Startwert oder der aktuellste Wert, negativ ist, lässt sich kein Ergebnis ermitteln.

	Gewinn 2013	Gewinn 2004	Wachstum 10 Jahre	innerer Wert
HeidelbergCement	3,98 €	-3,64 €	#WERT!	#WERT!
RWE ST	-4,49 €	3,80 €	#WERT!	#WERT!

Dieser Umstand verführt zu der Idee, statt der annualisierten Wachstumsrate die durchschnittliche Wachstumsrate einzusetzen. Dabei wird von Jahr zu Jahr die Wachstumsrate ermittelt und deren Mittelwert gebildet. Beträgt das Gewinnwachstum über Jahre beispielsweise 10%, 15% und 20%, so ergibt sich ein Mittelwert von (10% + 15% + 20%) : 3 = 15%.
Das sieht erst einmal gut aus, hat aber einen entscheidenden Nachteil:
Eine AG hat einen Gewinn pro Aktie über mehrere Jahre von 1,00 € , 0,01 € , 1,00€. Die annualisierte Wachstumsrate würde 0% betragen, da Start- und Endwert identisch sind.
Bei der durchschnittlichen Wachstumsrate würden die einzelnen Änderungsraten folgendermaßen aussehen:
Von 1,00 € auf 0,01 € => -99% – von 0,01 € auf 1,00 € => 9900%. Der Mittelwert würde 4900,5% betragen.
Ich denke wir sind uns einig, dass die Wachstumsrate der AG nicht über 4900% beträgt.

Problem 4:

In der Gewinn- und Verlustrechnung sind bilanztechnische Faktoren wie z.B. Abschreibungen und Rückstellungen enthalten, die das Ergebnis verfälschen können.
So kann der Gewinn durch die Bildung von einmaligen Rückstellungen u.U. stark absinken. Für den Gewinn der Folgejahre hat diese Maßnahme aber keinen Einfluss.

Lösungsansätze

Wir wollen zwei Möglichkeiten vorstellen, die oben aufgeführten Probleme zu umgehen oder abzuschwächen.

Die Verwendung des Umsatzes:
Der Umsatz ist nicht abhängig von der Art der Bilanzierung und von Sondereffekten. Zudem ist eine Berechnung immer möglich, da der Umsatz nie negativ sein kann.
Nachteilig ist die Tatsache, dass zwischen Umsatz und Gewinn kein streng linearer Zusammenhang steht. Häufig steigt bei höherem Umsatz der Gewinn überproportional an, falls die Gewinnschwelle bereits überschritten wurde (Thema: Fixkosten -„break-even point“).
Andererseits kann ein Umsatzanstieg z.B. auch durch Preissenkungen (Stichwort: „Dumpingpreise“ zur Erhöhung des Marktanteils) bedingt sein. In diesem Fall würde sich der Gewinn unterproportional zum Umsatz entwickeln.
Die Verwendung von Durchschnittsgewinnen
Benjamin Graham empfiehlt, die Wachstumsraten zu berechnen, indem die Durchschnittsgewinne der letzten drei Jahre mit dem Dreijahresdurchschnitts zu Beginn des Beobachtungszeitraums verglichen werden.

	Gewinn 2014e	Gewinn 2013	Gewinn 2012	Gewinn 2006	Gewinn 2005	Gewinn 2004	Ø-Gewinn 2012-2014	Ø-Gewinn 2004-2006	Wachstum	innerer Wert
Adidas	3,10 €	3,76 €	2,52 €	2,25 €	1,93 €	1,64 €	3,13 €	1,94 €	6,15%	64,46 €
Allianz	13,96 €	13,05 €	11,34 €	16,78 €	11,24 €	5,98 €	12,78 €	11,33 €	1,52%	161,00 €
BASF	5,38 €	5,27 €	5,31 €	3,19 €	2,87 €	1,72 €	5,32 €	2,59 €	9,40%	146,85 €
Bayer	4,65 €	3,86 €	2,96 €	2,22 €	2,19 €	0,83 €	3,82 €	1,75 €	10,29%	135,21 €
Beiersdorf	2,37 €	2,35 €	1,95 €	2,93 €	1,45 €	1,29 €	2,22 €	1,89 €	2,05%	29,87 €
BMW ST	9,04 €	8,10 €	7,77 €	4,38 €	3,33 €	3,30 €	8,30 €	3,67 €	10,74%	271,11 €

In unserem Beispiel wird der durchschnittliche Gewinn pro Aktie der Jahre 2012 bis 2014 mit dem der Jahre 2004 bis 2006 verglichen. Eingesetzt in die oben aufgeführte Formel für die jährliche Wachstumsrate erhalten wir für Adidas:

CAGR(2012-2014, 2004-2006) = (3,13 € / 1,94 €)^^1/8 – 1 = 0,06147 = 6,15%

Verwendung des errechneten inneren Wertes

Vom errechneten inneren Wert muss nun noch die Sicherheitsmarge abgezogen. Diese ist je nach Anleger und Einsatzzweck unterschiedlich.
Für das zukünftige Depot, das rein auf der Berechnung des inneren Wertes beruht (siehe weiter unten) wird eine hohe Sicherheitsmarge von 50% verwendet.
Im nächsten Artikel werden wir die Aktien auf eine Reihe von Kennzahlen hin untersuchen. Dabei ist der innere Wert nur einer von vielen Werten. Aus diesem Grund wird die Sicherheitsmarge auf 30% reduziert.

Fazit und Ausblick

Benjamin Graham stellt die Formel im Kapitel „Wertpapieranalyse für den Laien“ vor. Weiter bemerkt er, dass dabei kein Wert auf „wissenschaftliche Exaktheit“ gelegt wird.
Folglich muss sich der Anleger, der die Berechnung einsetzt, im Klaren sein, dass es sich nur um eine grobe Schätzung handeln kann. Der Zusammenstellung des Portfolios rein auf dieser Grundlage scheint somit nicht empfehlenswert, ist aber definitiv besser als ohne Strategie vorzugehen. Zumal die Sicherheitsmarge mögliche Abweichungen zu einem gewissen Grad ausgleichen kann.

Ab 2015 wird ein Depot auf Grundlage dieser Berechnung des inneren Wertes erfolgen. Das Depot wird in erster Linie als Vergleichsmaßstab zu anderen Value-Strategien gesehen. Dennoch bis ich sehr gespannt, wie die Strategie abschneidet, da in einer Studie von Dr. Hendrik Leber und J. Henrik Muhle die einfachen Value-Strategien häufig besser abgeschnitten haben.

Dez. 01

Anlagestrategie Value Investing

Von Mathias Maier unter Blog, Strategie

Value Investing ist eine Anlagestrategie, die in den frühen 1930er Jahren von Benjamin Graham entwickelt wurde.

Die Definition des Value Investing ist eng mit Auslegung des Begriffes der „Anlage“ verknüpft.
In seinem Buch „Security Analysis“ aus dem Jahre 1934 geht Graham auf den Unterschied zwischen einer Anlage und einer Spekulation ein:

„Eine Anlage ist eine Investition, die aufgrund einer Analyse für das Anlageobjekt Sicherheit verspricht sowie eine angemessene Rendite zusichert. Alle anderen Konzeptionen müssen als spekulatives Engagement angesehen werden.“

Was verbirgt sich hinter der Aussage? Lassen Sie uns den Inhalt einer genaueren Betrachtung unterziehen:

„aufgrund einer Analyse“ – Benjamin Graham fordert auch beim Erwerb von wenigen Aktien oder Anleihen, eine Analyse des betreffenden Unternehmens durchzuführen, als ob der Anleger die Firma komplett zu kaufen gedenke.
„Sicherheit sowie eine angemessene Rendite“ – was im Zusammenhang zu sehen ist.
Damit ein Wertpapier für einen Value Investor in Frage kommt, müssen eine Reihe von Kriterien bezüglich Kennzahlen wie z.B. KGV, KBV, Eigenkapital und Verschuldungsgrad, bezüglich Unternehmensgröße, Geschäftmodell, Produkten und Management etc. erfüllt sein.
Letztendlich muss der innere Wert (errechneter Wert) deutlich unterhalb des Kurswertes liegen.
„Alle anderen Konzeptionen … spekulativ …“ – Ein renommiertes,solides, gut geführtes und profitables Unternehmen ist nicht zwangsläufig ein Anlageobjekt für den Value Investor. Dazu muss das Unternehmen auch mit Preisabschlag zum inneren Wert gehandelt werden.

Grundannahme des Value Investing ist, dass die Märkte ineffizient sind. Um den Begriff des ineffizienten Marktes zu erklären, wenden wir uns der Definition der effizienten Märkte zu.

Die Theorie der effizienten Märkte

Der Wirtschaftswissenschaftler Eugene Fama stellte 1970 die Effizienzmarkthypothese (Efficient Market Hypothesis – EMH) vor. In einem effizienten Markt sind alle vorhandenen Informationen bereits in den Kursen enthalten. Das hat zur Folge, dass weder durch Technische Analyse, Fundamentalanalyse noch durch eine beliebige, andere Art von Analyse eine dauerhafte Überrendite gegenüber dem Gesamtmarkt erzielt werden kann, da der aktuelle Kurs immer dem inneren Wert entspricht.
Kritiker führen in erster Linie auf, dass sich in effizienten Märkten keine (Spekulations-)Blasen bilden dürften. Beispielsweise konnte ein Value Investor vor dem Platzen der Dotcom-Blase im Jahre 2000 feststellen, dass die Kurswerte des Großteils der börsennotierten Unternehmen dem inneren Wert weit vorausgeeilt waren. So war die Entwicklung des Value Investing durch Benjamin Graham eine direkte Folge der Weltwirtschaftskrise des Jahres 1929.

Kommen wir zu der Ausgangsstellung zurück, dass für einen Value Investor die Märkte ineffizient sind. Das hat zur Folge, dass der Aktienkurs eines Unternehmens, welches einen inneren Wert von 100 € hat, auf 130 € steigen kann. Selbst von diesem hohen Niveau aus kann die Aktie noch weiter steigen. Aber irgendwann wird die Überbewertung offensichtlich und der Kurs nähert sich dem inneren Wert an.
Umgekehrt kann die obige Aktie auch unter dem inneren Wert gehandelt werden. Fällt der Kurs auf 70 €, wird das Unternehmen für den Value Investor interessant, der mit einer Sicherheitsmarge von 30% arbeitet.
Die Höhe der Sicherheitmarge kann sich von Anleger zu Anleger unterscheiden, bzw. ein Anleger kann bei unterschiedlichen Firmengrößen oder unterschiedlichen Branchen mit differenzierten Sicherheitsabschlägen arbeiten.

Vor- und Nachteile des Value Investing

Vorteile:

Es ist möglich, eine überdurchschnittliche Rendite zu erzielen.
Minimiertes Risiko durch die Sicherheitsmarge bei einem diversifizierten Depot (nicht alles auf eine Karte setzen).
Value Investing ist keine Modeerscheinung, sondern eine bewährte Methode.

Nachteile:

Die Umsetzung der Strategie ist zeitaufwändig.
Zur Umsetzung müssen gewisse Kenntnisse über die Fundamentalanalyse vorhanden sein oder erworben werden.
Zur Ermittlung des inneren Werts müssen Schätzungen über zukünftige Entwicklungen getroffen werden. Dabei wußte schon Mark Twain:“Prognosen sind schwierig, besonders wenn sie die Zukunft betreffen.“
Die Strategie erfordert eine längerfristige Anlagedauer. Bis sich der Kurs dem inneren Wert annähert können u.U. Jahre vergehen.
Während beispielsweise bei der Dividendenstrategie „Dogs of the Dow“ eine feste Handlungsanweisung vorgegeben wird, die Emotionen ausschließt, muss der Value Anleger einen Weg finden, objektiv zu agieren.

Fazit:

Value Investing ist für den erfahrenen Anleger, der bereit ist Zeit aufzuwenden, eine sehr effektive Anlageform.
Wer vom Konzept überzeugt ist, aber nicht die Zeit oder die Kenntnisse zur Umsetzung hat, findet die Möglichkeit in entsprechende Fonds zu investieren oder auf professionelle Dienstleistungen zurückzugreifen.

Wie geht es weiter:

Diese Thematik ist zu umfangreich, um sie in einem Artikel zu erschlagen. Deswegen soll im weiteren Verlauf die Überprüfung von Aktien anhand von Kennzahlen und Eigenschaften der Unternehmen vorgestellt werden. Dabei wird auch eine einfache Formel von Benjamin Graham zur Ermittlung des inneren Wertes erläutert.
Weiter werden wir uns mit dem CROCI-Verfahren (von der Deutschen Bank entwickelt) in einer einfachen und der ausführlichen Variante beschäftigen.
Von ausgewählten Werten werden wir den inneren Wert mit der Discounted-CashFlow-Methode ermitteln. Außerdem werden für den Januar verschiedene Depot der einzelnen Verfahren zusammengestellt, um die zukünftige Entwicklung verfolgen zu können.

Nov. 23

Untersuchung zu weiteren 200-Tage-Linien Strategien

Von Mathias Maier unter Blog, Strategie

(auf Grafik klicken zum Vergrößern)

Ein großer Nachteil der 200-Tage-Linien Strategie ist – wie bereits erwähnt – die Gefahr von häufigen Fehlsignalen, vor allem in Seitwärtsmärkten.
Deshalb wurde schon immer nach Möglichkeiten gesucht, die Strategie zu optimieren. Oftmals wird in diesem Zusammenhang ein zweiter, kürzer gleitender Durchschnitt in Kombination mit der 200-Tage-Linie eingesetzt.
Gängige Werte sind der 38-, 50- und 65-Tage-Durchschnitt.
Die Umsetzung ist denkbar einfach: durchbricht die kürzerperiodische Linie (z.B. die 38-Tage-Linie) die 200-Tage-Linie nach oben, so wird ein Kaufsignal erzeugt. Erfolgt der Durchbruch nach unten, wird ein Verkaufssignal generiert.
In der Charttechnik bezeichnet der Begriff „Todeskreuz“ das Durchschneiden der 50-Tage-Linie unter die 200-Tage -Linie.

Im weiteren Verlauf werden die Kombinationen der 200-Tage-Linie mit der 38-Tage-Linie, der 50-Tage-Linie, der 65-Tage-Linie und der 90-Tage-Linie über einen Zeitraum von sieben Jahren hinweg bezüglich der jeweiligen Performance untersucht. Wie schon bei der vorausgegangenen Untersuchung werden die Variationen nochmals aufgeteilt in eine reine Long-Variante und eine Long- und Short-Variante.
Bei der Long-Variante werden nach einem Kaufsignal DAX-ETFs erworben, die sich 1:1 wie der DAX-Index bewegen. Erfolgt ein Verkaufssignal, werden die DAX-ETFs in Bargeld umgeschichtet.
Bei der Long- und Short-Variante werden ebenfalls DAX-ETFs nach einem Kaufsignal bezogen. Nach einem Verkaufssignal wird allerdings in Short-ETFs umgeschichtet, die sich gegenläufig zum DAX-Index entwickeln.

Der aufgeführte Vergleich bezieht sich auf den Zeitraum vom 1.01.2007 bis zum 30.12.2013. Für die Untersuchung wurde der DAX-ETF mit der Wertpapierkennnummer DBX1DA für die Umsetzung der Kaufsignale eingesetzt. Als Short-ETFs – falls von der Variante her gefordert – wurde das Papier mit der WPKN DBX1DS verwendet. Wie bei den Depots werden für die Kauf- und Verkaufsgebühren 0,1% des Wertes plus 9 € berechnet.
Zusätzlich sind noch die Ergebnisse der Varianten aufgeführt, die für die 200-Tage-Linien Strategie verwendet werden (200-Tage-Linie inklusive 3%-Toleranz).

Typ	Bezeichnung	Startwert absolut	Endwert absolut	Rendite absolut [%]	Rendite jährlich [%]

1a	GD 200 – GD 38 ohne Short	20.000,00 €	29.692,43 €	48,46%	5,81%
1b	GD 200 – GD 38 mit Short	20.000,00 €	25.841,03 €	29,21%	3,73%
2a	GD 200 – GD 50 ohne Short	20.000,00 €	30.625,32 €	53,13%	6,28%
2b	GD 200 – GD 50 mit Short	20.000,00 €	27.999,59 €	40,00%	4,92%
3a	GD 200 – GD 65 ohne Short	20.000,00 €	32.431,91 €	62,16%	7,15%
3b	GD 200 – GD 65 mit Short	20.000,00 €	31.763,34 €	58,82%	6,83%
4a	GD 200 – GD 90 ohne Short	20.000,00 €	30.610,34 €	53,05%	6,27%
4b	GD 200 – GD 90 mit Short	20.000,00 €	28.205,52 €	41,03%	5,03%
5	DAX Buy-and-Hold	6614,73	9552,16	44,41%	5,39%
6a	mit 3%-Toleranz ohne Short	20.000,00 €	34.389,76 €	71,95%	8,05%
6b	mit 3%-Toleranz inkl. Short	20.000,00 €	38.490,90 €	92,45%	9,80%

Zwei Punkte fallen sofort ins Auge:

Bei der Verwendung zweier gleitender Durchschnitte schneiden alle Varianten mit Short-Anteil schlechter ab als die Varianten mit reinem Long-Anteil (im Gegensatz zur Standard 200-Tage-Linien Strategie mit 3%-Toleranz).
Am besten schneidet die Kombination aus 200-Tage-Linie und 65-Tage-Linie ab, aber auch diese Spielart erreicht nicht die Rendite der Standard 200-Tage-Linien Strategie mit 3%-Toleranz.

Typ	Bezeichnung	Anzahl Käufe	Anzahl Verkäufe	Anteil Tage Long [%]	Anteil Tage Short [%]	Anteil Tage nicht investiert [%]

1a	GD 200 – GD 38 ohne Short	3	2	56,84%	0,00%	43,16%
1b	GD 200 – GD 38 mit Short	3	3	56,84%	27,97%	15,19%
2a	GD 200 – GD 50 ohne Short	3	2	56,45%	0,00%	43,55%
2b	GD 200 – GD 50 mit Short	3	3	56,45%	28,42%	15,13%
3a	GD 200 – GD 65 ohne Short	3	2	55,44%	0,00%	43,44%
3b	GD 200 – GD 65 mit Short	3	3	55,44%	28,14%	15,30%
4a	GD 200 – GD 90 ohne Short	2	1	55,83%	0,00%	44,11%
4b	GD 200 – GD 90 mit Short	2	2	55,83%	28,48%	15,64%
5a	mit 3%-Toleranz ohne Short	3	2	57,34%	0,00%	42,66%
5b	mit 3%-Toleranz inkl. Short	3	3	57,34%	27,91%	14,74%

Auch bezogen auf die Anzahl der Kauf- und Verkaufssignale bieten die Modifikationen keine Optimierung, zumindest in Bezug auf die 200-Tage-Linien Strategie mit Toleranz.

Tendenziell kommt auch ein Performance-Test der FAZ.net im Artikel „Gleitende Durchschnitte helfen dabei den Markt zu schlagen“ zu ähnlichen Ergebnissen.
Zu beachten ist, dass in dem Test der Bezugsindex der S&P 500 ist, und dass die 200-Tages-Linien Strategie ohne Toleranz getestet wurde.

Zuletzt soll noch ein Blick auf einen verkürzten 4-Jahres Zeitraum (2010 bis 2013) geworfen werden, in dem kein Bärenmarkt auftrat.

Typ	Bezeichnung	Startwert absolut	Endwert absolut	Rendite absolut [%]	Rendite jährlich [%]

1a	GD 200 – GD 38 ohne Short	20.000,00 €	26.123,25 €	30,62%	6,91%
1b	GD 200 – GD 38 mit Short	20.000,00 €	19.322,72 €	-3,39%	-0,86%
2a	GD 200 – GD 50 ohne Short	20.000,00 €	25.453,16 €	27,27%	6,21%
2b	GD 200 – GD 50 mit Short	20.000,00 €	18.332,26 €	-8,34%	-2,15%
3a	GD 200 – GD 65 ohne Short	20.000,00 €	26.479,97 €	32,40%	7,27%
3b	GD 200 – GD 65 mit Short	20.000,00 €	20.598,80 €	2,99%	0,74%
4a	GD 200 – GD 90 ohne Short	20.000,00 €	26.746,07 €	33,73%	7,54%
4b	GD 200 – GD 90 mit Short	20.000,00 €	19.795,47 €	-1,02%	-0,26%
5	DAX Buy-and-Hold	5975,42	9552,16	59,86%	12,44%
6a	mit 3%-Toleranz ohne Short	20.000,00 €	29.761,08 €	48,81%	10,45%
6b	mit 3%-Toleranz inkl. Short	20.000,00 €	38.490,90 €	92,45%	9,80%

Die oben getroffenen Aussagen werden auch für den verkürzten Beobachtungszeitraum bestätigt.

Fazit:

Die durchgeführten Untersuchungen geben keinen Hinweis darauf, dass die Varianten mit zwei gleitenden Durchschnitten eine bessere Rendite als die vorgestellte 200-Tage-Linien Strategie ermöglichen.
Somit besteht auch kein Bedarf, eine diese Modifikationen in einem Depot umzusetzen.

Nov. 18

200-Tage-Linien-Strategie

Von Mathias Maier unter Blog, Strategie

Die 200-Tage-Linien-Strategie ist als trendfolgende Strategie der technischen Analyse zuzuordnen.

Als Signalgeber dient der einfache gleitende Durchschnitt (simple moving average) der letzten 200 Tage.

Um die Anzahl der Fehlsignale zu verringern, wird mit einem Toleranzfenster von 3% gearbeitet, da diese Variante in der „Untersuchung zur 200-Tage-Linien Strategie“ die überzeugendsten Ergebnisse lieferte.

Ferner werden zwei Variationen angeboten: Einmal werden nur „Long“-Positionen eingegangen, d.h. nach Kaufsignalen ist das Depot voll mit Standard-ETFs investiert, bei Verkaufssignalen wird das Pulver in Form von Bargeld trocken gehalten. Diese Variante schneidet in Seitwärtsmärkten besser ab.
Zum anderen werden „Long“ und „Short“ Positionen eingegangen. Nach Kaufsignalen wird wie zuvor agiert, bei Verkaufssignalen wird in Short-ETFs investiert, deren Kurswert sich bei fallendem DAX erhöht (und umgekehrt). Diese Variante bringt in Bärenmärkten hohe Renditen.

Die Regeln der 200-Tage-Linie Strategie (Long)

Einen Index auswählen (wir beziehen uns hier und in den Musterdepots auf den DAX-Performance-Index).
Steigt der Index mindestens 3% über den gleitenden Durchschnitt der letzten 200-Tage, werden DAX-ETFs gekauft.
Fällt der Index mindestens 3% unter die 200-Tage-Linie, so werden die Papiere verkauft. Bis zum nächsten Kaufsignal werden keine neuen Investitionen vorgenommen.

Die Regeln der 200-Tage-Linie Strategie (Long und Short)

Einen Index auswählen (wir beziehen uns hier und in den Musterdepots auf den DAX-Performance-Index).
Steigt der Index mindestens 3% über den gleitenden Durchschnitt der letzten 200-Tage, werden eventuell im Depot befindliche Short-ETFs verkauft und DAX-ETFs gekauft.
Fällt der Index mindestens 3% unter die 200-Tage-Linie, so werden die Papiere verkauft. Stattdessen werden Short-ETFs auf den DAX-Performance-Index erworben.

Vor- und Nachteile der 200-Tage-Linien Strategien

Nachteile:

In Seitwärtsmärkten kann sich eine Reihe von Fehlsignalen bilden, die sich negativ auf die Performance niederschlagen.
Durch den Einsatz des gleitenden Durchschnitts über 200 Tage können die Signale erst mit Verzögerung gebildet werden.

Vorteile:

Die Strategie ist leicht verständlich und einfach nachzuvollziehen.
Die Umsetzung erfordert nur einen geringen Zeitaufwand.
Eine Verlustbegrenzung ist für jeden Handel in der Strategie integriert (durch die entsprechenden Verkaufssignale).
Durch den Einsatz von ETFs ist die Strategie auch mit kleinem Kapitaleinsatz sinnvoll (somit auch als Depotbeimischung).
Durch die klaren Regeln ist die Strategie frei von Emotionen.

Performance der Strategie

Auch hier gilt: Renditen aus der Vergangenheit sind keine Garantie für Renditen in der Zukunft.
Der DAX (Performance-Index inklusive Dividenden) stieg zwischen 2007 und 2013 jährlich um durchschnittlich 5,4 %. Im gleichen Zeitraum erzielte die “200-Tage-Linien”-Strategie Long (mit 3%-Toleranz) eine jährliche Rendite von 8,05 % und die “200-Tage-Linien”-Strategie Long und Short 9,8 %.

Sehen wir uns näher an, was aus 10.000 € Startkapital mit diesen Renditen geworden wäre:

Bezug	Strategie	Zeitraum	Jährliche Rendite	Start-kapital	Kapital am Ende des Zeitraums

DAX	Buy and Hold	2007-2013	5,39%	10.000 €	14.441 €
DAX	200-Tage Long	2007-2013	8,05%	10.000 €	17.195 €
DAX	200-Tage Long und Short	2007-2013	9,80%	10.000 €	19.245 €

Nov. 16

Untersuchung zur 200-Tage-Linien Strategie

Von Mathias Maier unter Blog, Strategie

Nach „boerse.ARD.de“ ist die 200-Tage-Linie das Maß aller Dinge. Sie ist ein einfaches Mittel um Trends zu erkennen, was auch ihre Bekanntheit und Beliebtheit erklärt.

Die 200-Tage-Linie ist ein „einfach gleitender Durchschnitt“ (GD200 oder SMA200 für simple moving average), d.h. es wird der Mittelwert aus den letzten 200 Handelstagen gebildet.

Mit diesem gleitenden Durchschnitt läßt sich eine Anlagestrategie umsetzen:
Schneidet der Kurs des DAX die 200-Tage-Linie von unten nach oben, so wird ein Kaufsignal generiert. Umgekehrt wird ein Verkaufssignal gebildet, wenn der Kurswert die Linie von oben nach unten kreuzt.

Liegt aber kein klarer Trend vor, so können viele kurzfristige Fehlsignale auftreten. Da an der Börse immer gilt: „Hin und her macht Beutel leer“, gibt es zahlreiche Modifikationen der Strategie, um die Performance zu erhöhen.

Im weiteren Verlauf wird untersucht, wie vier Varianten der 200-Tage-Linien Strategie in der Vergangenheit abgeschnitten haben. Zudem wird jede Variante nochmals unterteilt. Zum einen wird bei einem Verkaufssignal in Bargeld umgeschichtet, zum anderen wird in diesem Fall in ein Short-ETF auf den DAX gekauft.

Folgende Varianten werden untersucht:

Standardumsetzung mit sofortigem Kauf, bzw. Verkauf bei Durchschreiten der Linie (Typ 1).
Ein Kaufsignal erfolgt erst nach Überschreitung der 200-Tage-Linie um 3%. Ein Verkaufssignal wird erst nach Unterschreitung um 3% wirksam (Typ 2).
Um ein Kaufsignal zu generieren muss die 200-Tage-Linie mindestens drei Tage in Folge überschritten bleiben. Entsprechend erfolgt ein Verkaufssignal erst, wenn die Linie mindestens drei Tage in Folge unterschritten bleibt (Typ 3).
Standardumsetzung mit sofortigem Kauf bei Überschreiten einer aufsteigenden 200-Tage-Linie, bzw. sofortiger Verkauf bei Unterschreiten einer absteigenden 200-Tage-Linie (Typ 4).

Typ	Bezeichnung	Startwert absolut	Endwert absolut	Rendite absolut [%]	Rendite jährlich [%]

1a	Standard ohne Short	20.000,00 €	32.596,67 €	62,98%	7,23%
1b	Standard inkl. Short	20.000,00 €	34.606,59 €	73,03%	8,15%
2a	mit 3%-Toleranz ohne Short	20.000,00 €	34.389,76 €	71,95%	8,05%
2b	mit 3%-Toleranz inkl. Short	20.000,00 €	38.490,90 €	92,45%	9,80%
3a	mit 3-Tage-Toleranz ohne Short	20.000,00 €	28.901,05 €	44,51%	5,40%
3b	mit 3-Tage-Toleranz inkl. Short	20.000,00 €	22.696,76 €	13,48%	1,82%
4a	Standard mit Auswertung der Richtung ohne Short	20.000,00 €	31.877,29 €	59,39%	6,89%
4b	Standard mit Auswertung der Richtung inkl. Short	20.000,00 €	24.015,53 €	20,08%	2,65%
5	DAX Buy-and-Hold	6614,73	9552,16	44,41%	5,39%

Typ	Bezeichnung	Anzahl Käufe	Anzahl Verkäufe	Anteil Tage Long [%]	Anteil Tage Short [%]	Anteil Tage nicht investiert [%]

1a	Standard ohne Short	11	10	57,40%	0,00%	42,60%
1b	Standard inkl. Short	11	11	57,40%	27,91%	14,69%
2a	mit 3%-Toleranz ohne Short	3	2	57,34%	0,00%	42,66%
2b	mit 3%-Toleranz inkl. Short	3	3	57,34%	27,91%	14,74%
3a	mit 3-Tage-Toleranz ohne Short	7	6	57,57%	0,00%	42,43%
3b	mit 3-Tage-Toleranz inkl. Short	7	7	57,57%	27,58%	14,85%
4a	Standard mit Auswertung der Richtung ohne Short	1	0	52,30%	0,00%	47,70%
4b	Standard mit Auswertung der Richtung inkl. Short	1	1	52,30%	12,61%	35,09%

Die Standard-Strategie schneidet deutlich besser ab als der DAX. Eine noch bessere Rendite bringt die Strategie in Verbindung mit einer 3%-Toleranz. Statt 11 Transaktionen kommt der Anleger hier mit 3 Transaktionen über den kopmpletten Zeitraum aus.
Beide Strategien zeigen mit dem Einsatz von Short-ETFs eine bessere Performance aus als einfach nach einem Verkaufssignal das Bargeld zu halten.
Nicht überzeugen konnte die Strategie mit der 3-Tage-Toleranz, da die Anzahl der Fehlsignale deutlich höher ist als im Vergleich zur 3%-Toleranz.
Sehr wenige Transaktionen müssen bei der Strategie mit der Betrachtung der Richtung des gleitenden Durchschnitts ausgeführt werden. Allerdings kommen SIgnale dadurch auch stark verzögert, was sich vor allem im Zusammenhang mit dem Einsatz von Short-ETFs negativ bemerkbar macht.

Deutlich die Nase vorne haben die 3%-Toleranz- und die Standard-Strategie. Beide in Verbindung mit Short-ETFs.
Ein Blick auf das obige DAX-Diagramm zwischen 2007 und 2013 zeigt, dass mit der Finanzkrise 2008 ein rund 15-monatiger Bärenmarkt in die Untersuchung mit eingeht. Die Tatsache wirft die Frage auf, ob die Anlage in Short-ETFs auch ohne eine explizite Baisse befriedigend abschneidet.
Aus diesem Grund wurde zusätzlich noch das Abschneiden in den Jahren 2010 bis 2013 untersucht.

In diesem Zeitraum sind deutlich Korrekturen zu erkennen wie z.B. ab Juli 2011, aber kein ausgeprägter Bärenmarkt.
In den beiden folgenden Tabellen sind die Ergebnisse aufgeführt.

Typ	Bezeichnung	Startwert absolut	Endwert absolut	Rendite absolut [%]	Rendite jährlich [%]

1a	Standard ohne Short	20.000,00 €	28.722,66 €	43,61%	9,47%
1b	Standard inkl. Short	20.000,00 €	23.811,46 €	19,06%	4,46%
2a	mit 3%-Toleranz ohne Short	20.000,00 €	29.761,08 €	48,81%	10,45%
2b	mit 3%-Toleranz inkl. Short	20.000,00 €	25.717,97 €	28,59%	6,49%
3a	mit 3-Tage-Toleranz ohne Short	20.000,00 €	25.172,35 €	25,86%	5,92%
3b	mit 3-Tage-Toleranz inkl. Short	20.000,00 €	19.358,51 €	-3,21%	-0,81%
4a	Standard mit Auswertung der Richtung ohne Short	20.000,00 €	31.877,29 €	59,39%	12,36%
4b	Standard mit Auswertung der Richtung inkl. Short	20.000,00 €	31.877,29 €	59,39%	12,36%
5	DAX Buy-and-Hold	5975,42	9552,16	59,86%	12,44%

Typ	Bezeichnung	Anzahl Käufe	Anzahl Verkäufe	Anteil Tage Long [%]	Anteil Tage Short [%]	Anteil Tage nicht investiert [%]

1a	Standard ohne Short	8	7	76,69%	0,00%	23,02%
1b	Standard inkl. Short	8	8	76,69%	14,50%	8,52%
2a	mit 3%-Toleranz ohne Short	3	2	76,69%	0,00%	23,31%
2b	mit 3%-Toleranz inkl. Short	3	2	76,69%	14,69%	8,62%
3a	mit 3-Tage-Toleranz ohne Short	6	5	76,69%	0,00%	23,31%
3b	mit 3-Tage-Toleranz inkl. Short	6	5	76,69%	14,40%	8,91%
4a	Standard mit Auswertung der Richtung ohne Short	1	0	91,38%	0,00%	8,62%
4b	Standard mit Auswertung der Richtung inkl. Short	1	0	91,38%	0,00%	8,62%

Erneut nicht überzeugen kann die Strategie mit der 3-Tage-Toleranz, bei der für die Short-Variante sogar ein Verlust anfällt.
Die 3%-Toleranz-Strategie schneidet erneut besser ab als die Standardstrategie, wobei diesmal die Short-Varianten schlechter abschneiden, da keine Bärenmarkt im Beobachtungszeitraum vorhanden ist.
Die beste Performance liefert die Strategie mit der Auswertung der Richtung des gleitenden Durchschnitts. Durch die starke Verzögerung der Signalbildung erfolgte hier kein Verkaufsignal, was sich in dem unter Schwankungen steigenden Markt positiv auswirkte.
Dennoch wird diese Variante aus zwei Gründen nicht mit in das Depot aufgenommen:

1. Durch die sehr verzögerte Signalgenerierung wird bei Trendwechseln zu spät reagiert.

2. Es war ein Zufall, dass im Auswertungszeitraum relativ schnell ein Signal ausgelöst wurde.
Unter Umständen können Jahre vergehen, ehe der Einstieg erfolgen kann.

Wegweisend für die 200-Tage-Linien Strategien ist die Tatsache, dass in letzterem Zeitraum die „Buy and Hold“-Strategie die beste Rendite erzielte. In unterschiedlichen Marktphasen können die Ergebnisse stark voneinander abweichen.

Im nächsten Diagramm wird die Entwicklung des Depotwertes beispielhaft an der Standard-Strategie mit Short-ETFs über den Zeitraum von 7 Jahren dargestellt.

Die Wertentwicklung kann in drei übergeordnete Bereiche eingeteilt werden:

Bereich 1: Das Depot besteht nur aus Bargeld, da noch kein Signal erzeugt wurde.

Bereich 2: Der Depotwert steigt deutlich an, da ein eindeutiger Trend vorhanden ist (2a: Abwärtstrend , 2b und 2c Aufwärtstrend.

Bereich 3: Der Depotwert schwankt, bzw. sinkt bei einem Seitwärtstrend mit vielen Signalwechseln.

In Summe konnte die Strategie mit der 3%-Toleranz am meisten überzeugen. Die Variante ohne Short-Anteil ist für Anleger geeignet, die von einer tendenziell positiven Entwicklung ausgehen. Die Variante mit Short-ETFs macht Sinn, wenn davon ausgegangen ist, dass Bullen- und Bärenmärkte sich häufiger abwechseln werden.

Im nächsten Artikel werden beide Strategien nochmals genau vorgestellt. Ferner werden beide Varianten in das Depot aufgenommen.

Nov. 11

Portfolio-Optimierung mit OpenOffice Calc

Von Mathias Maier unter Blog, Wissen

Im letzten Artikel wurden Risiko und Rendite eines Portfolios mit fünf Aktien berechnet. Dabei wurden alle Aktien mit 20% gewichtet.

Zur Portfolio-Optimierung müssen – je nach persönlichem Ziel – die einzelnen Komponenten unterschiedlich gewichtet sein.
Natürlich können Sie einfach unterschiedliche Werte ausprobieren und das Ergebnis betrachten. Wirklich effektiv ist diese Methode jedoch nicht, wie folgendes Beispiel erkennen läßt:

In einer früheren Auswertung mit einem anderen Portfolio wurden alle Möglichkeiten der Gewichtung in 10%-Stufen festgelegt.

In OpenOffice Calc sieht der Aufbau folgendermaßen aus:

In Spalte „N“ besteht das Portfolio zu 100% aus Adidas-Aktien. In Spalte „O“ beträgt der Anteil der Adidas-Aktien 90%, hinzu kommen 10% Allianz-Aktien.
Um alle Varianten auszuspielen, werden mehr als 1000 Spalten benötigt. Dabei ist die Schrittweite von 10% für die praktische Umsetzung zu groß. Wollen wir eine geringere Schrittweite von beispielsweise 1% oder eine Portfolio mit mehr Einzelwerten, ist diese Art der Auswertung nicht mehr zu bewältigen.

Wesentlich geeigneter für das Arbeiten mit unterschiedlichen Gewichtungen ist die Monte-Carlo-Simulation, die bereits im Zusammenhang mit dem „Value at Risk„ erwähnt wurde.
Bei der Monte-Carlo-Simulation werden Zufallszahlen für die jeweiligen Anteile des Portfoliobestandes gebildet. Dabei muss die Bedingung erfüllt sein, dass alle Anteile zusammen 100% ergeben.
Von diesen Zufallsreihen werden nun etliche Tausende ermittelt, um eine ausreichende Anzahl an Variationen zur Verfügung zu haben.
Die Datenreihen samt Ergebnissen im Bezug auf Risiko und Rendite können danach auf die gewünschten Informationen hin gefiltert und ausgewertet werden.
Zu einem späteren Zeitpunkt werden wir diese Methode in einem separaten Artikel umsetzen.

Portfolio-Optimierung mit dem Solver

Moderne Tabellenkalkulationsprogramme wie Excel und OpenOffice Calc bieten mit dem „Solver“ ein mächtiges Tool an. Der „Solver“ (deutsch: Löser) ist eine erweiterte Zielwertsuche, bei der der gesuchte Wert in Abhängigkeit von mehreren Nebenbedingungen ermittelt werden kann.
In Excel steht der „Solver“ als „Add-In“ zur Verfügung, welches unter „Extras“ / „Add-Ins“ vor dem ersten Einsatz installiert werden muss.

OpenOffice Calc stellt standardmäßig einen „Solver“ bei, allerdings nur für lineare Gleichungssysteme. Um alle Möglichkeiten nutzen zu können, müssen wir eine Extension für nichtlineare Gleichungssysteme nachrüsten.
Wir wollen den kostenlosen „Solver for Nonlinear Programming [Beta]“ einsetzen, der hier zum Download zur Verfügung steht.

Nach einem Klick auf den Button „Download extension“ öffnet sich eine neue Seite, in der folgende Dialogbox erscheint:

Am einfachsten lässt sich die Installation über die Auswahl „Öffnen mit OpenOffice“ durchführen. Die Extension wird automatisch in OpenOffice eingebunden.

Aufgerufen wird der „Solver“ über „Extras“ / „Sover“.

Zum Prüfen, ob die Extension installiert wurde, gehen Sie auf „Optionen“ und öffnen das Listenfeld unter „Solver Engine“. Hier müssen nun drei „Solver“ zur Auswahl stehen.

Wählen Sie den „DEPS Evolutionary Algorithm“ aus.

Für die weiteren Ausführungen verwenden wir wieder die im letzten Artikel erstellte Datei „Portfolio_5_Aktien.ods“.
Bevor wir mit dem Solver fortfahren, müssen wir in der Tabelle „Berechnung“ noch ein Feld ergänzen.

Eine Voraussetzung, die wir im „Solver“ einsetzen, ist, dass die Summe aller Gewichtungen „1“ (100%) ergibt. Diese Berechnung führen wir in der Zelle C8 aus.

Nun wollen wir den „Solver“ einsetzen. Die erste Aufgabe soll die Bestimmung der größten zu erwartenden Rendite sein.
Dazu starten wir den „Solver“ über „Extras“ / „Sover“ und machen folgende Eingaben, bzw. Vorwahlen:

Die Zielzelle beinhaltet den Wert, den wir beeinflussen wollen. In diesem Fall ist es die Rendite.
Zielwert ist das Maximum, da wir die höchste Rendite suchen.
Die veränderbaren Zellen sind die jeweiligen Gewichtungen (C3:C7 oder als Name „w“), da wir wissen wollen, bei welchen Gewichtungen die höchste Rendite zu erwarten ist.
Als erste Nebenbedingung definieren wir, dass die einzelnen Anteile nicht größer als „1“ (100%) sein dürfen.
Als zweite Nebenbedingung legen wir fest, dass die einzelnen Anteile nicht negativ sein dürfen. Prinzipiell sind auch negative Werte bis „-1“ möglich. In diesem Fall würde mit Verkaufsoptionen gearbeitet. Da es zu vielen Papieren aber keine entsprechenden Verkaufsoptionen gibt, bzw. nicht jeder Zugang zu dieser Art von Wertpapieren hat, verzichten wir auf diese Variante.
Als dritte Nebenbedingung wird bestimmt, dass die Summe der Gewichtungen „1“ (100%) betragen muss.

Zur Ausgabe des Ergebnisses drücken Sie den Button „Lösen“. Der „Solver“ führt die Berechnungen aus.

Mit „OK“ wird die Berechnung abgeschlossen und Sie werden gefragt, ob Sie die Ergebnisse in Ihre Tabelle übernehmen wollen.

Übernehmen Sie die Daten.

Werfen wir einen Blick auf das Ergebnis:

Als Resultat erhalten wir ein Portfolio, das zu 100% aus BMW-Aktien besteht. Das Ergebnis kann nicht wirklich überraschen, wenn wir uns daran erinnern, dass die Rendite eine lineare Funktion ist. Die höchste Rendite erzielen wir, wenn wir nur den Wert mit der höchsten Rendite einsetzen.
Aber Ziel der Portfolio-Theorie ist die Reduzierung des Risikos bei akzeptabler Rendite. Mit nur einem Titel tragen wir jedoch das komplette, unsystematische (diversifizierbare) Risiko.

Minimum-Varianz Portfolio

Als Nächstes wollen wir das Minimum-Varianz Portfolio (MVP) bestimmen. Das MVP ist das Portfolio mit dem geringsten Risiko.
Dazu öffnen wir erneut den „Solver“ und ändern zwei Werte.

Zunächst wählen wir als Zielzelle die Standardabweichung (Zelle B13). Die Varianz wäre als Zielzelle ebenfalls möglich, da Standardabweichung und Varianz in direktem Zusammenhang stehen.
Die zweite Änderung betrifft den Zielwert. Hier wählen wir „Minimum“, da der kleinste Wert gesucht wird.

Nach Lösen der Gleichung und Durchlauf aller 2000 Berechnungsschritte erhalten wir folgendes Ergebnis.

Durch die Änderung der Gewichtung in 0% BMW, 57,58% Beiersdorf, 2,31% Deutsche Bank, 17,03% E.ON und 23,07% SAP kann das Risiko von 8,08% auf 3,68% mehr als halbiert werden. Gleichzeitig sinkt die Rendite um weniger als ein Drittel.

Der effiziente Rand

Der effiziente Rand beschreibt die Kurve vom Minimum-Varianz Portfolio zum Portfolio mit der höchsten Rendite für die zu jedem Wert der Standardabweichung keine höhere Rendite möglich ist.
Wir wollen nun den effizienten Rand unseres Portfolios bestimmen. Dazu tragen wir einmal die Standardabweichung und die Rendite für das Portfolio mit der höchsten Rendite ein, danach die Werte des MVP.

Jetzt haben wir die äußeren Begrenzungen der Kurve. Weitere Punkte legen wir fest, indem wir für die Standardabweichungen 0,04 – 0,045 – 0,05 etc. bis 0,075 die höchsten Renditen berechnen.

Dafür wählen wir wieder die Rendite als Zielzelle und „Maximum“ als Zielwert. Als vierte Nebenbedingung fügen wir den gewünschten Sollwert der Standardabweichung hinzu. Allerdings verwenden wir nicht den Operator „=“ sondern „<=“. Bei „=“ wird ganz genau der Wert „0,4000000“ gefordert, was u.U. zu keiner Lösung führt.
Die Berechnungen werden für alle Werte der vorgegebenen Standardabweichungen ausgeführt und die Werte in der Tabelle ergänzt.

Den besten Überblick bietet ein Diagramm. Unter „Einfügen“ / „Diagramm“ wird das Streudiagramm ausgewählt. Wir erhalten folgendes Ergebnis:

Je mehr Zwischenwerte errechnet werden, desto genauer wird die Kurve.
Allerdings läßt sich schon deutlich erkennen, dass nach dem linken Punkt (MVP) ein steiler Anstieg der Rendite erfolgt, der im weiteren Verlauf immer mehr abflacht.
Das bedeutet, dass im Bereich der Standardabweichung von 0,04 bis 0,05 ein sehr gutes Chance-Risiko Verhältnis für dieses Portfolio besteht. Danach werden kleine Renditesprünge mit deutlicher Erhöhung des Risikos erkauft.

Hinweis:

Der Artikel beschreibt nur die Möglichkeit, wie die Optimierung eines Portfolios mit dem „Solver“ durchgeführt werden kann.
Wer sich der Portfolio-Theorie verschreibt, wird nie ein Portfolio aufbauen, das nur aus Werten des DAX besteht.

Bei einer größeren Anlagesumme besteht die Möglichkeit eine Diversifikation durch Aktien unterschiedlicher Branchen, Regionen und Marktkapitalisierungen. Neben der notwendigen Kapitalbasis ist hierfür auch ein entsprechender Zeitaufwand zu kalkulieren.

Einfacher und mit weniger Startkapital lässt sich ein optimiertes Portfolio mit ETFs, Index- und Themenzertifikaten und Fonds (etwas kostspieliger) umsetzen.

Je nach Risikoneigung sollten auch Anleihen mit hoher Bonität zur Senkung des Risikos eingesetzt werden.

Nov. 07

Portfolio-Berechnungen mit OpenOffice Calc

Von Mathias Maier unter Blog, Wissen

Bisher war die Optimierung im Bezug auf Risiko und Rendite auf zwei Aktien begrenzt. In der Praxis kommen wir mit zwei Werten nicht wirklich weiter.

In diesem Artikel werden wir mittels OpenOffice Calc und den integrierten Matrix-Funktionen die Berechnung auf eine erweiterte Anzahl von Titeln erhöhen. Im konkreten Beispiel arbeiten wir mit fünf Aktien, aber mit der gleichen Vorgehensweise können wir beliebig viele Wertpapiere einbeziehen.

Die Handlungsanweisungen und Funktionen lassen sich in dieser Form auch in Excel umsetzen.

Dazu erstellen wir eine neue OpenOffice-Datei mit dem Namen „Portfolio_5_Aktien.ods“. Die Kursdaten und Renditeberechnungen kopieren wir aus der zuvor erstellten Datei „Risiko_Rendite.ods“ und fügen sie in das aktuelle Projekt ein.

Zur besseren Nachvollziehbarkeit geben wir dem Tabellenblatt den Namen „Daten“. Nun wenden wir uns der zweiten Tabelle zu und vergeben den Namen „Berechnung“ (mit rechter Maustaste auf den Reiter klicken, „Tabelle umbenennen“ wählen und neuen Namen eingeben).

Um Schreibarbeit zu vermeiden, werden wir eine Funktion anwenden, die wir auch im weiteren Verlauf einsetzen werden: das Transponieren.
Wie bereits im Artikel „Ein kurzer Ausflug in die Matrix-Algebra“ beschrieben, werden durch das Transponieren die Zeilen und Spalten einer Matrix vertauscht.Klingt kompliziert, ist aber mit einem Tabellenkalkulationsprogramm einfach umzusetzen:
Dazu gehen wir wieder zur ersten Tabelle („Daten“), markieren die Zellen B2 bis F2 mit den Namen der Aktien und vergeben im oberen, linken Feld, das den Zellbereich angibt, den Namen „Aktien“.

Wir wechseln zur Tabelle „Berechnung“ und markieren die Zellen A3 bis A7. Die Funktion zum Transponieren lautet „MTRANS“. Entsprechend müssen wir „=MTRANS(Aktien)“ eingeben.

WICHTIG!!!

Damit das Programm erkennt, dass es sich um eine Matrix-Formel handelt, muss die Eingabe mit „<Strg>+<Shift>+<ENTER>“ abgeschlossen werden.
Anhand der geschweiften Klammer um die Formel, läßt sich erkennen, dass die Formel als Matrix verabeitet wird.

Im nächsten Schritt vergeben wir die Überschriften. In Spalte B wollen wir die erwarteten Renditen ausgeben, die häufig mit dem griechischen Buchstaben „μ“ (sprich: mü) angegeben werden. Diese Bezeichnung wollen wir an dieser Stelle ebenfalls verwenden (über „Einfügen“ – „Sonderzeichen“).
In Spalte C geben wir die Gewichtung der einzelnen Positionen an. Hierzu verwenden wir die Bezeichnung „w“.

Die zu erwartende Rendite für jede der Aktien haben wir bereits in der Tabelle „Daten“ errechnet. Wir werden die Werte an dieser Stelle wieder über die Funktion „Transponieren“ einlesen.
Dazu wechseln wir wieder zur Tabelle „Daten“, markieren die Renditen in den Zellen H52 bis L52 und vergeben den Namen „E_Rendite“.

In der Tabelle „Berechnung“ markieren wir die Zellen B3 bis B7, geben die bekannte Formel „=MTRANS(E_Rendite)“ ein und beenden die Eingabe mit „<Strg>+<Shift>+<ENTER>“.

Für die Gewichtung vergeben wir für alle Aktien den Wert 0,2, d.h. jede Aktie soll einen Anteil am Portfolio von 20% haben. Gerne können Sie auch die Ausgabe in Prozent formatieren, so dass in jedem Feld der Wert 20% erscheint. Für die Berechnung ist dies unerheblich, da 0,2 und 20% vom reinen Zahlenwert identisch sind.

Danach vergeben wir unterhalb die Bezeichnungen für die Berechnungen des Gesamtportfolios.

Zur Berechnung der erwarteten Rendite werden wieder Namen für Zellbereiche eingegeben. Zum einen werden die fünf Einzelrenditen mit „mue“, zum anderen die Gewichtungen der Aktien mit „w“ bezeichnet.

Berechnung der Portfolio-Rendite

Schauen wir uns beide Matrizen an, stellen wir fest, dass es sich beidesmal um eine 5×1-Matrix handelt. In unserem Ausflug in die Matrix-Algebra hatten wir aber festgestellt, dass eine 5×1-Matrix nicht mit einer 5×1-Matrix multipliziert werden kann (5x1 * 5x1 => die beiden rot dargestellten Zahlen sind ungleich, daraus folgt, dass keine Matrix-Multiplikation möglich ist).
Sehr wohl kann aber eine 5×1-Matrix mit einer 1×5-Matrix multipliziert werden (1×5 * 5×1 => die beiden grün dargestellten Zahlen sind gleich, daraus folgt, dass die Matrix-Multiplikation möglich ist).
Wie aus einer 5×1-Matrix eine 1×5-Matrix wird, ist uns in der Zwischenzeit bekannt: durch Transponieren der Matrix mittels der Funktion „MTRANS“.
Somit lautet die Formel für die erwartete Portfolio-Rendite:

E(_rp) = w^T * μ w^T steht für w transponiert

In OpenOffice Calc lautet die Funktion für die Matrix-Multiplikation „MMULT“. Somit sieht die komplette Formel wie folgt aus:

=MMULT(MTRANS(w); mue)

Wir erhalten einen Wert von 0,0068 (auf 4 Nachkommastellen formatiert) oder 0,68% erwartete, monatliche Rendite.

Berechnung der Portfolio-Varianz

Die Formel zur Berechnung der Portfolio-Varianz lautet:

$Var = w^{T} Sw$

Die Gewichtung „w“ – auch in transponierter Form – ist bekannt.
Neu dadegen ist „S“, die Varianz-Kovarianz-Matrix. Sie wird wie folgt berechnet:

$S = \dfrac{A^{T} * A}{M - 1}$

Dabei bezieht sich „A“ auf die periodischen Renditen bezogen auf die mittlere Rendite.
Bei BMW beispielsweise beträgt die erwartete Rendite (mittlere Rendite) über den Beobachtungszeitraum 1,26%. Beträgt die Rendite für eine Periode 2,26%, so wäre der Wert bezogen auf die mittlere Rendite 1 % (2,26% – 1,26%). Liegt die periodische Rendite unter der mittleren Rendite, ist der Wert negativ. Wäre die Rendite einer Periode 0,26%, ergibt sich ein Wert von -1% (0,26% – 1,26%).

Zur Umsetzung kopieren wir die Überschriften der Zellen H bis L , fügen sie im Bereich N bis R ein und ändern den Text der zellübergreifenden Überschrift auf „monatliche Rendite bezogen auf den Mittelwert“.

Danach markieren wir alle Datenzellen der monatlichen Renditen von H3 bis L49 und vergeben für den Bereich den Namen „P_Rendite“ (periodische Renditen).

Zur Berechnung der Renditen bezogen auf den Mittelwert setzen wir wieder die Matrix-Algebra ein. Dazu markieren wir die Zellen N3:R49 und subtrahieren von den periodischen Renditen (P_Rendite) die erwartete (mittlere) Rendite, die wir bereits zuvor mit „E_Rendite“ bezeichnet haben.

Somit lautet die Formel für unsere Berechnung:

Da es sich um eine Matrix-Berechnung handelt, muss die Formel mit „<Strg>+<Shift>+<ENTER>“ abgeschlossen werden.

Anschließend vergeben wir für den gesamten Bereich den Namen „A“.

Werfen wir noch einmal einen Blick auf die Formel der Varianz-Kovarianz-Matrix S:

$S = \dfrac{A^{T} * A}{M - 1}$

Es ist nur noch „M – 1“ offen. „M“ ist die Anzahl der beobachteten periodischen Renditen, in unserem Fall 47 (H3:H49). Somit ergibt M – 1 = 46.
Diesen Wert tragen wir in unsere Tabelle „Berechnungen“ ein und vergeben für die Zelle F1 den Namen „Perioden“.

Nun sind wir in der Lage die Varianz-Kovarianz-Matrix S zu erstellen.
Wir kopieren die Bezeichnungen der Aktien in Spalte A und fügen sie in Spalte G ein.

Nun müssen die Bezeichnungen noch in Zeile 2 eingefügt werden.
Spalten in Zeilen können wir einfach durch Transponieren einfügen. An dieser Stelle möchte ich eine zweite Möglichkeit zum Transponieren zeigen:

Kopieren Sie die Zellen G3 bis G7
Markieren Sie die Zellen H2 bis L2
Drücken Sie die rechte Maustaste und wählen „Inhalte einfügen“ aus.

Wählen Sie die Option „Transponieren“ und bestätigen mit „OK“.

Die Aktiennamen werden nun in die Zeile übernommen.

Jetzt müssen wir die Matrix nach der oben erwähnten Formel mit Inhalten füllen:

Wir führen eine Matrixmultiplikation mit „A“ transponiert und „A“ durch und teilen das Ergebnis durch die Anzahl der Werte minus 1 (=Perioden). Nach „<Strg>+<Shift>+<ENTER>“ sieht das Ergebnis wie folgt aus:

Wir können einfach überprüfen, ob unsere Berechnungen korrekt waren. Die farblich gekennzeichneten Werte müssen den Varianzen entsprechen, die wir in der Tabelle „Daten“ errechnet haben:

In diesem Fall stimmen die Ergebnisse überein.

Somit stehen wir kurz vor dem Ziel. Wir müssen für die Varianz-Kovarianz-Matrix (H3:L7) noch den Namen „S“ vergeben, ehe wir uns der Varianz des Gesamtportfolios zuwenden können.

Die Formel war:

$Var = w^{T} Sw$

Im Gegensatz zu einer üblichen Zahlenmultiplikation läßt sich eine Matrix-Multiplikation nicht in der Form A*B*C durchführen. Stattdessen müssen zwei Multiplikationen nacheinander ausgeführt werden:
Die erste Multiplikation innerhalb der Klammer ist „MMULT(MTRANS(w); S)“.
In der zweiten wird obige Multiplikation nochmals mit „w“ multipliziert, wodurch der komplette Ausdruck lautet:

„=MMULT(MMULT(MTRANS(w); S); w)“

Wie immer bei einer Matrix-Funktion muss die Eingabe mit „<Strg>+<Shift>+<ENTER>“ beendet werden.

Die Standardabweichung unseres Portfolios ist die Wurzel der Varianz.

Wir sind nun in der Lage die erwartete Rendite und die Standardabweichung eines Portfolios aus mehr als zwei Aktien zu berechnen.
Sie können nun ein wenig experimentieren, welche Änderungen sich bei unterschiedlichen Gewichtungen „w“ ergeben.

Im nächsten Artikel werden wir darauf eingehen, wie die Gewichtungen für ein optimales Portfolio mit den vorgegebenen Werten errechnet werden können.

Nov. 02

Ein kurzer Ausflug in die Matrix-Algebra

Von Mathias Maier unter Blog, Wissen

Zuletzt haben wir nur Portfolios mit zwei Aktien untersucht. Um das unsystematische (oder diversifizierbare) Risiko weitgehend auszuschließen, reichen zwei Werte definitiv nicht aus.

Wollen wir aber die bisher eingesetzten Berechnungen auf ein Portfolio von fünf oder gar zehn Aktien erweitern, stoßen wir auf Grenzen. Zwar ist die Berechnung prinzipiell möglich, doch nehmen die Formeln immer monströsere Ausmaße an.

Mit Hilfe der Matrix-Algebra lassen sich die Berechnungen wesentlich einfacher und eleganter durchführen.

Da im nächsten Tutorial die Matrix-Algebra eingesetzt wird, erfolgt in diesem Artikel eine kurze Einführung in die Materie.

Sie können dieses Kapitel gerne überspringen und die spätere Vorgehensweise einfach kopieren. Falls Sie aber den Vorgang nachvollziehen wollen, empfehle ich Ihnen weiterzulesen.

Einführung in die Matrix-Algebra

Eine Matrix ist eine rechteckige Anordnung (Tabelle) von reellen Zahlen, die entsprechend ihrer Größe als „m x n„ (sprich m mal n) – Matrix bezeichnet wird. Dabei gilt:

m = Anzahl der Zeilen

n = Anzahl der Spalten

Die einfachste Form ist uns allen gut bekannt. Die „1 x 1“-Matrizen (auch als Skalare bezeichnet) sind reelle Zahlen, mit denen wir im alltäglichen Leben rechnen.

Weiter Sonderformen sind:

Die „m x 1“-Matrix, der sogenannte Spaltenvektor $\begin{bmatrix} 1\\ 2\\ 3\end{bmatrix}$

Die „1 x n“-Matrix, der sogenannte Zeilenvektor $\begin{bmatrix} 1 & 2 & 3\end{bmatrix}$

Eine zweidimensionale Matrix A, z.B. in Form einer „3 x 2“-Matrix, sieht wie folgt aus:

$A =\begin{bmatrix} 1 & 4\\ 2 & 5\\ 3 & 6\end{bmatrix}$

Die transponierte Matrix

Eine Matrix deren Zeilen und Spalten vertauscht wurden, wird als transponierte Matrix bezeichnet.
Aus der oben verwendeten „3 x 2“-Matrix wird somit eine „2 x 3“-Matrix:

$A =\begin{bmatrix} 1 & 4\\ 2 & 5\\ 3 & 6\end{bmatrix}$ => $A^T =\begin{bmatrix} 1 & 2 & 3\\ 4 & 5 & 6\end{bmatrix}$

Das Transponieren einer Matrix werden wir für unsere Portfolio-Berechnungen desöfteren einsetzen.

Die Addition von Matrizen

Eine Matrizen-Addition läßt sich nur ausführen, wenn die Dimensionen der zu addierenden Matrizen gleich groß sind. Eine „3 x 2“-Matrix kann nur mit einer „3 x 2“-Matrix addiert werden.

$A =\begin{bmatrix} 1 & 4\\ 2 & 5\\ 3 & 6\end{bmatrix}$ $B =\begin{bmatrix} 11 & 14\\ 12 & 15\\ 13 & 17\end{bmatrix}$ $A+B =\begin{bmatrix} 1+11 & 4+14\\ 2+12 & 5+15\\ 3+13 & 6+16\end{bmatrix}=\begin{bmatrix} 12 & 18\\ 14 & 20\\ 16 & 22\end{bmatrix}$

Für die Subtraktion von Matrizen gelten die selben Regeln.

Die Multiplikation von Matrizen

Die Multiplikation von 3 Äpfeln * 2 Birnen ergibt nicht 6 Apfelbirnen. Diese Multiplikation macht keinen Sinn. Haben wir aber 3 Kisten mit jeweils 3 Äpfeln und 2 Birnen, können wir eine Multiplikation in Form von 3 * 3 Äpfeln = 9 Äpfeln, sowie 3 * 2 Birnen = 6 Birnen durchführen.

Auch die Multiplikation von Matrizen macht nur Sinn, wenn gewisse Bedingungen erfüllt sind. Lassen Sie uns zwei Matrizen multiplizieren:

„m₁ x n₁“ * „m₂ x n₂„

Matrix 1 hat m₁ Zeilen und n₁ Spalten, Matrix 2 hat m₂ Zeilen und n₂ Spalten.
Eine Multiplikation ist unter der Bedingung möglich, dass n₁ = m₂, d.h. die Anzahl der Spalten in Matrix 1 muss gleich der Anzahl der Zeilen in Matrix 2 sein.
Ferner gibt m₁ die Anzahl der Zeilen und n₂ die Anzahl der Spalten des Ergebnisses aus.
Dazu drei Beispiele:

$A =\begin{bmatrix} 1 & 2 & 3\end{bmatrix}$ und $B =\begin{bmatrix} 1\\ 2\end{bmatrix}$

„1 x 3“ * „2 x 1″

Matrix 1 hat 3 Spalten, während Matrix 2 nur 2 Spalten hat. Eine Multiplikation ist nicht möglich.

$A =\begin{bmatrix} 1 & 2 & 3\end{bmatrix}$ und $B =\begin{bmatrix} 1\\ 2\\ 3\end{bmatrix}$

„1 x 3“ * „3 x 1″

Matrix 1 hat 3 Spalten und Matrix 2 hat 3 Zeilen, somit ist eine Multiplikation möglich. Das Ergebnis ist eine „1 x 1“-Matrix.

$A =\begin{bmatrix} 1 & 2\end{bmatrix}$ und $B =\begin{bmatrix} 3 & 5\\ 4 & 6\end{bmatrix}$

„1 x 2“ * „2 x 2″

Matrix 1 hat 2 Spalten und Matrix 2 hat 2 Zeilen, somit ist eine Multiplikation möglich. Das Ergebnis ist eine „1 x 2“-Matrix.

Wann wir multiplizieren können ist nun bekannt. Stellt sich die Frage nach dem „Wie“.
Dazu verwenden wir die beiden Beispiele, bei denen die Rechnung möglich ist:

$A =\begin{bmatrix} 1 & 2 & 3\end{bmatrix}$ und $B =\begin{bmatrix} 1\\ 2\\ 3\end{bmatrix}$ => $A * B =\begin{bmatrix} 1 & 2 & 3\end{bmatrix} \begin{bmatrix} 1\\ 2\\ 3\end{bmatrix} =\begin{bmatrix} 1*1 + 2*2 + 3*3\end{bmatrix} =\begin{bmatrix} 14\end{bmatrix}$

Der erste Wert des Zeilenvektors A wird mit dem ersten Wert des Spaltenvektors B multipliziert, anschließend der zweite Wert von A mit dem zweiten Wert von B und der dritte Wert von A mit dem dritten Wert von B. Die einzelnen Ergebnisse werden addiert.

$A =\begin{bmatrix} 1 & 2\end{bmatrix}$ und $B =\begin{bmatrix} 3 & 5\\ 4 & 6\end{bmatrix}$ => $A * B =\begin{bmatrix} 1 & 2\end{bmatrix} \begin{bmatrix} 3 & 5\\ 4 & 6\end{bmatrix} =\begin{bmatrix} 1*3 + 2*4 & 1*5 + 2*6\end{bmatrix} =\begin{bmatrix} 11 &17\end{bmatrix}$

Der erste Wert der Matrix A wird mit jedem Wert der Spalte 1 von Matrix B multipliziert, die Ergebnisse werden addiert und bilden den Wert der Spalte 1.Der zweite Wert der Matrix A wird mit jedem Wert der Spalte 2 von Matrix B multipliziert, die Ergebnisse werden addiert und bilden den Wert der Spalte 2.

Mit diesen Informationen sind wir gerüstet, die Portfolio-Berechnungen in der Praxis durchzuführen.

Okt. 26

Risiko-Rendite-Diagramme mit OpenOffice Calc

Von Mathias Maier unter Blog, Wissen

Nachdem wir zuletzt die Rendite, Varianz, Standardabweichung und Korrelation verschiedener Wertpapiere berechnet haben, wollen wir in diesem Artikel „Risiko-Rendite“-Diagramme erstellen.

Als Grundlage verwenden wir wieder die OpenOffice Calc-Datei „Risiko_Rendite.ods“, die im Artikel „Korrelation mit OpenOffice Calc berechnen“ erstellt wurde.

Das Risiko-Rendite-Diagramm wird mit zwei Aktienpaaren erstellt. Wir wollen mit der Paarung BMW ST – SAP beginnen, die die höchste Korrelation aufweist. Anschließend wollen wir uns Beiersdorf – E.On zuwenden. Dieses Paar weist die geringste Korrelation auf.

Zuerst vergeben wir Überschriften für zwei Spalten. In der ersten Spalte werden die Gewichtungen für die BMW-Aktie, in der zweiten Spalte die Gewichtungen für die SAP-Aktie eingetragen.

Unterhalb der Bezeichnungen werden beide Spalten zur besseren Übersichtlichkeit als Prozentangaben mit zwei Nachkommastellen formatiert.

Wir setzen für die Gewichtung 5%-Schritte ein, d.h. der erste Wert der BMW-Aktie ist 0,00%, der zweite Wert 5,00%. Nun markieren wir beide Zellen, gehen mit der Maus auf das kleine, schwarze Quadrat (der Mauszeiger verwandelt sich dabei in ein „+“) und ziehen die Maus bei gedrückter linker Maustaste nach unten bis 100% erreicht werden.

Bei der SAP-Aktie starten wir mit 100%, da die Summe beider Anteile im Portfolio 100% sein muss. Der zweite Wert ist 95%. Danach können wir wieder beide Werte markieren und über das schwarze Quadrat die Wert bis 0% übernehmen. Diese Vorgehensweise läßt auch ohne große Schreibarbeit kleinere Schritte, z.B. im 1%-Bereich zu.

Das Ergebnis sieht nun wie folgt aus:

Zur Erstellung des Risiko-Rendite-Diagramms sind zwei weitere Spalten erforderlich. Sinnigerweise das Risiko in Form der Standardabweichung und die Rendite in Form des Mittelwertes der periodischen Renditen.

Beginnen wollen wir mit dem einfacheren Teil – der Rendite. Die Rendite ist eine lineare Funktion. Ist die Gewichtung beider Aktien beispielweise 50%, so wird 0,5 mal die Rendite der BMW-Aktie berechnet plus 0,5 mal die Rendite der SAP-Aktie. Bei einem Verhältnis von 10% zu 90% wird 0,1 mal die Rendite von BMW plus 0,9 mal die Rendite von SAP berechnet.
In OpenOffice Calc sieht die Funktion wie folgt aus:

In der Formel stehen die Zellen „N5“ und „O5“ für die Gewichtungen beider Aktienanteile, die Zellen „H52“ und „L52“ für die mittleren monatlichen Renditen von BMW bzw. SAP.
Da die Gewichtung bei 100% SAP-Anteile liegt, entspricht die Rendite derjenigen der SAP-Aktie.
Für die Ausgabe der Renditen mit den weiteren Gewichtungen müssen wir in die Formel noch etwas bearbeiten. Durch ein „$“-Zeichen vor den Zeilennummern der mittleren, monatlichen Renditen stellen wir sicher, dass immer auf die selbe Zelle zugegriffen wird:
Die Formel hat nun folgenden Inhalt: „=N5*H$52+O5*L$52“.
Jetzt verwenden wir wieder das schwarze Quadrat der markierten, ersten Zelle der Renditeberechung und ziehen es bis zum Ende der Berechnungen.
Die zweite Zelle hat somit folgendes Aussehen:

Die Gewichtungen werden für die Folgezeilen übernommen, während der Bezug zur Rendite der beiden Wertpapiere gleich bleibt.

Die Formel der Standardabweichung für ein Portfolio aus zwei oder mehr Aktien ist etwas umfangreicher, da keine Linearität zwischen den einzelnen Standardabweichungen besteht (mit einer Ausnahme: Korrelation=1).
Was sich zunächst negativ anhört, ist auf den zweiten Blick ein Glücksfall. Denn nur Dank dieser Tatsache läßt sich das Risiko eines Portfolios bei gleicher Rendite verringern.
Zur Berechnung der Standardabweichung müssen wir den Umweg über die Varianz gehen. Die Formel für den Fall mit zwei Aktien lautet:

Var_p = x₁² * σ₁² + x₂² * σ₂² + 2 * x₁ * x₂ * σ₁ * σ₂ * ρ_1,2

Dabei ist

x₁, x₂ : Gewichtung Aktie 1 und Aktie 2 [0..1]

σ₁, σ₂ : Standardabweichung Aktie 1 und Aktie 2

ρ_1,2 : Korrelation der beiden Aktien [-1..1]

Die Standardabweichung ist die Wurzel der Varianz. In OpenOffice Calc sieht die Formel folgendermaßen aus:

N5 und O5 sind die Gewichtungen, H54 und L54 die Standardabweichungen und L57 die Korrelation zwischen der BMW- und der SAP-Aktie.
Jetzt werden wir die Formel wieder mit Konstanten versehen, um die Funktionen für die weiteren Zellen übernehmen zu können. Nicht verändert werden dürfen die Standardabweichungen und die Korrelation:

=WURZEL(N5^2*H$54^2+O5^2*L$54^2+2*N5*O5*H$54*L$54*L$57)

Nach Übernahme der Funktionen über das schwarze Quadrat sehen die Daten wie folgt aus:

Zur besseren Nachvollziebarkeit der Berechnungen sehen Sie nachfolgend noch einen Auszug aus der Tabelle. Durch einen Klick auf die Grafik wird diese vergrößert.

Bild „Berechnungsergebnisse“

Im nächsten Schritt erstellen wir das Diagramm. Dazu markieren wir die Datenfelder der Standardabweichung und der Rendite inklusive der Überschriften und wählen im Menü „Einfügen“ – „Diagramm“.

Es öffnet sich der Diagramm-Assistent, in dem wir folgende Auswahlen treffen:
Als Diagrammtyp verwenden wir das „XY-Streudiagramm“ mit Punkten, wobei Sie gerne auch Punke und Linien oder nur Linien auswählen können.

Über den „Weiter>>“-Button kommen wir zum Datenbereich. Hier wählen wir „Datenreihen in Spalten“ aus.

Die Eingaben zum Punkt „Datenreihen“ können wir beibehalten.

Zuletzt können wir Titel, Untertitel und Legenden beschriften und bei Bedarf die gewünschten Gitter anzeigen.

Das Diagramm sieht dann in der Weise aus:

Einiges an Arbeit können wir uns bei der Erstellung des zweiten Diagramms sparen, indem wir die Zellen, die wir für das erste Diagramm verwendet haben, kopieren und unterhalb einfügen.
Danach ersetzen wir BMW ST durch Beiersdorf und SAP durch E.ON.

Werfen wir nun einen Blick auf die Risikokomponente, sprich: die Standardabweichung.

Für die Gewichtung sind schon die korrekten Zellen mit „N31“ und „O31“ übernommen worden. Aber „H$54“ weist auf die Standardabweichung von BMW, die durch die Standardabweichung von Beiersdorf („I$54“) ersetzt werden muss. Gleiches gilt für „L$54“ (Standardabweichung von SAP). Dieser Verweis muss auf „K$54“ (Standardabweichung E.ON) lauten.

Zuletzt muss die Korrelation „L$57“ (Korrelation zwischen BMW SAP) durch die Korrelation zwischen Beiersdorf und E.ON („K$58“) ersetzt werden.
Die Formel der Bearbeitungsleiste sieht nun folgendermaßen aus:

=WURZEL(N31^2*I$54^2+O31^2*K$54^2+2*N31*O31*I$54*K$54*K$58)

Zum besseren Verständnis der Zellbezüge werfen Sie bitte nochmals einen Blick auf das Bild „Berechnungsergebnisse“ weiter oben.

Das gleiche Spiel wiederholen wir für die Rendite:

Hier müssen wir lediglich die monatliche Rendite von BMW („H$52“) durch die von Beiersdorf („I$52“) und die Rendite von SAP („L$52“) durch die von E.ON („K$52“) ersetzen:

=N31*I$52+O31*K$52

Nun markieren wir die beiden überarbeiteten Zellen und übernehmen die Daten für die weiteren Felder (schwarzes Quadrat).

Über „Einfügen“ – „Diagramm“ geben wir das Diagramm mit den Einstellungen von oben aus. Lediglich der Untertitel muss angepaßt werden, da wir ein anderes Aktienpaar verwenden.

Von den fünf Aktien, deren Kurse wir eingelesen haben, können wir im Moment immer nur zwei Aktien im Bezug auf Risiko und Rendite untersuchen. Im nächsten Artikel wollen wir das Portfolio mit allen fünf Aktien überprüfen.

Okt. 19

Autokredit

Von T. F. unter Service

Finanzierungsmöglichkeiten beim Kauf eines Autos

Neben einem Kredit werden Leasingverträge immer beliebter. Vor allem werden Leasingverträge weitaus einfacher vergeben als Kredite. Zwar wird auch hier auf das Einkommen und die Schufa geachtet. Dennoch werden Zusagen für ein Leasing weitaus rascher vergeben als für andere Darlehen. Wer sich ein Auto mittels Leasing finanzieren möchte, der sollte bedenken, dass es sich im Grunde genommen um eine Miete handelt. Monatlich werden die vereinbarten Raten zurückerstattet und am Ende des Leasingvertrages wird dann noch der Restwert bezahlt.

Mehr zu diesem Thema im kostenlosen E-Book Autokredit bei www.kreditzentrale.com.

Wie finanzieren sich Selbstständige ihre Fahrzeuge?

Für Selbstständige ist es oftmals schwieriger einen Kredit zu bekommen. Zwar stimmt das monatlich Einkommen in den meisten Fällen, den Banken ist allerdings die wirtschaftliche Lage oftmals nicht sicher genug. Immerhin können private Unternehmen und Firmen von heute auf morgen rote Zahlen schreiben. Der Autokredit für Selbständige gestaltet sich demnach in den meisten Fällen durchaus schwierig. Das ist mitunter auch ein Grund weswegen Selbstständige immer wieder auf das Leasing zurückgreifen. So können Fahrzeuge vorfinanziert werden. Ebenso ergibt sich bei einem Leasingvertrag auch eine steuerliche Entlastung, welche sich bei der Barzahlung eines Wagens nicht ergeben würde.

Kommentar hinterlassen