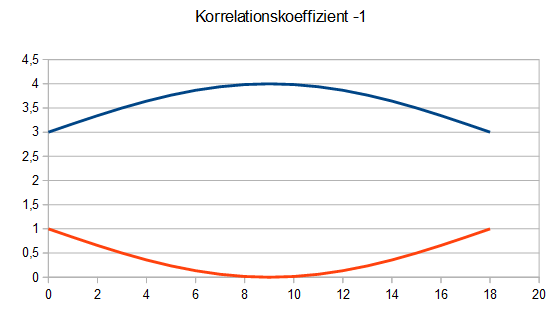
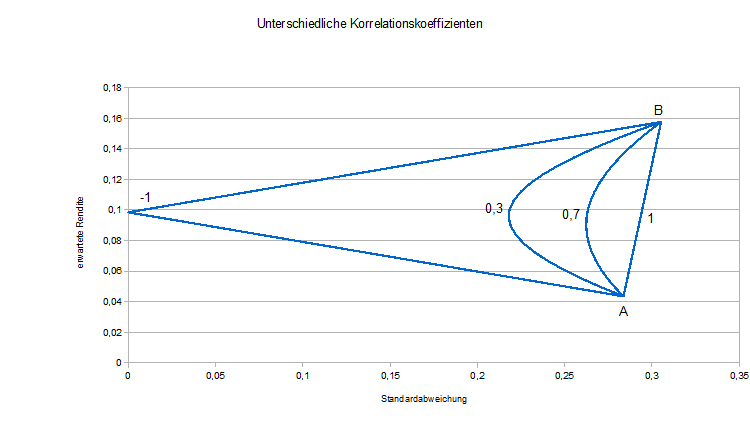
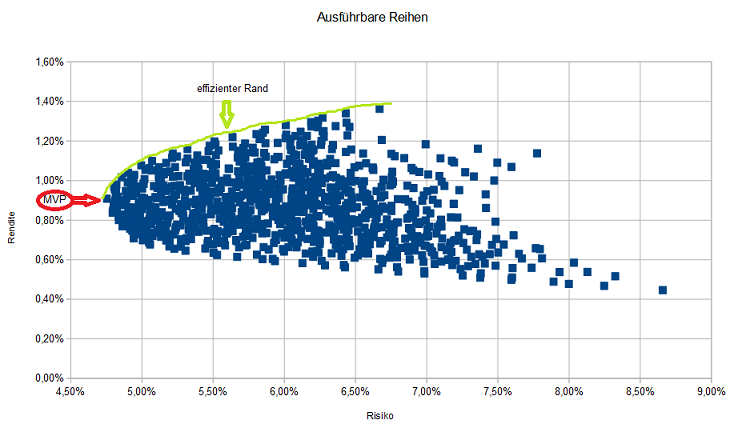
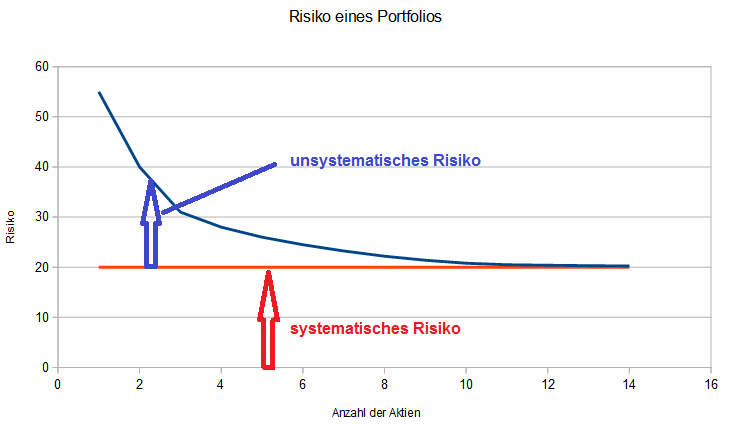
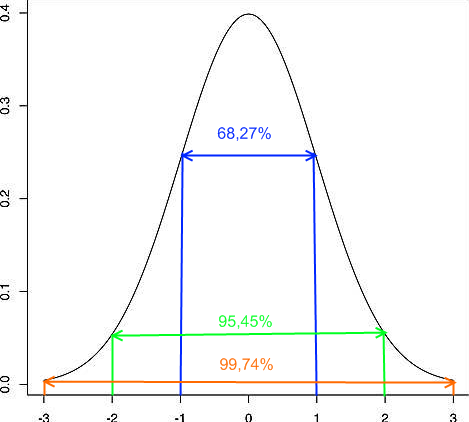
In diesem Artikel wird die Korrelation zwischen 5 Aktien unterschiedlicher Branchen des DAX-Index‘ berechnet.
In diesem Artikel wird die Korrelation zwischen 5 Aktien unterschiedlicher Branchen des DAX-Index‘ berechnet.
Eingesetzt wird das kostenlose Open Source Tabellenkalkulationsprogramm „OpenOffice Calc“.
Unter Excel sind die Funktionen und Berechnungen identisch. Lediglich das Handling kann sich unterscheiden.
Die Daten und Tabellen werden auch als Grundlage zur Portfoliooptimierung dienen, die im Nachfolgeartikel vorgestellt wird.
Die Berechnung der Korrelation erfolgt in vier Schritten:
- Die Kursdaten der Aktien beschaffen und in Tabelle integrieren.
- Die Renditen der einzelnen Perioden berechnen.
- Die zu erwartende Rendite, die Varianz und die Standardabweichung berechnen.
- Die Korrelationen zwischen den einzelnen Werten berechnen.
Folgende fünf Aktien werden für die Berechnungen verwendet:
- BMW ST als zyklischer Automobiltitel
- Beiersdorf als Konsumwert
- Die Deutsche Bank als Finanz- /Bankwert
- E.ON als Versorger
- SAP als Softwaretitel
Kursdaten der Aktien
In diesem Beispiel werden wir den Zeitraum der letzten vier Jahre zur Berechnung verwenden. Dazu reichen die monatlichen Schlußkurse der einzelnen Wertpapiere aus.
Prinzipiell wäre es ohne sehr großen Mehraufwand auch möglich, die Wochen- oder Tagesschlußkurse zu verwenden. Statt 48 Datenreihen müssten dann 208 bzw. über 1000 Werte importiert werden.
Während bei Tagesschlußkursen eine große Auswahl an Portalen vorhanden ist, die es ermöglicht, die Daten im „csv“-Format herunterzuladen (beispielsweise Onvista oder Ariva ), ist das Angebot bei den Wochen- und Monatsschlußkursen deutlich eingeschränkt. Wir werden diese Daten von Yahoo Finance Deutschland beziehen.
Am Beispiel unserer ersten Aktie BMW ST (WKN 519000) sieht das wie folgt aus:
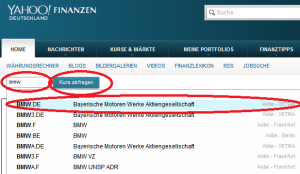 Leider ist bei Yahoo Finance nur die Suche über das Symbol möglich. Wertpapierkennnummer oder ISIN werden als Eingabe nicht akzeptiert. Doch üblicherweise ist es durch die Eingabe der ersten Buchstaben des Namens und dem sich öffnenden Auswahlfensters relativ einfach, die gewünschte Aktie zu finden. Sollte es in Ausnahmefällen nicht zum Erfolg finden, bietet sich als Hilfe das Wallstreet-Online Portal an. Hier können Sie die Aktie auf die übliche Art und Weise suchen und erhalten zusätzlich die Angabe des Symbols:
Leider ist bei Yahoo Finance nur die Suche über das Symbol möglich. Wertpapierkennnummer oder ISIN werden als Eingabe nicht akzeptiert. Doch üblicherweise ist es durch die Eingabe der ersten Buchstaben des Namens und dem sich öffnenden Auswahlfensters relativ einfach, die gewünschte Aktie zu finden. Sollte es in Ausnahmefällen nicht zum Erfolg finden, bietet sich als Hilfe das Wallstreet-Online Portal an. Hier können Sie die Aktie auf die übliche Art und Weise suchen und erhalten zusätzlich die Angabe des Symbols:
In unserem Beispiel öffnet sich nach Eingabe von „BMW“ nebenstehendes Auswahlfenster, in dem wir „BMW.DE“ für den XETRA-Kurs selektieren oder das Symbol eintragen und den Button „Kurs abfragen“ betätigen.
Neben dem Namen des Wertpapiers und des Symbols wird auch die WKN und ISIN angezeigt, so dass Sie überprüfen könne, ob Sie auch die korrekte Auswahl getroffen haben.
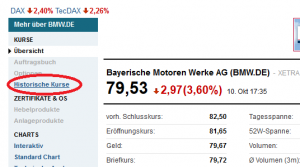
Wir befinden uns nun auf der Übersichtsseite der Aktie. Zu den Kursdaten gelangen wir über die Auswahl „Historische Kurse“ im linken Menüfeld.
Wir können nun festlegen, welche Kursdaten wir verwenden wollen. In unserem Fall ist dies „Monatlich“, da wir nur ein Kurs pro Monat einsetzen. Dazu kommt der Zeitraum vom 1.11.2010 bis zum 1.10.2014 (bei monatlichen Daten gibt Yahoo immer den ersten Tag eines Monats an).
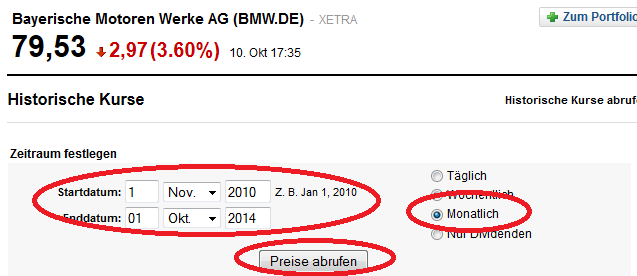 Mit einem Klick auf „Preise abrufen“ werden die gewünschten Daten darunter angezeigt:
Mit einem Klick auf „Preise abrufen“ werden die gewünschten Daten darunter angezeigt:
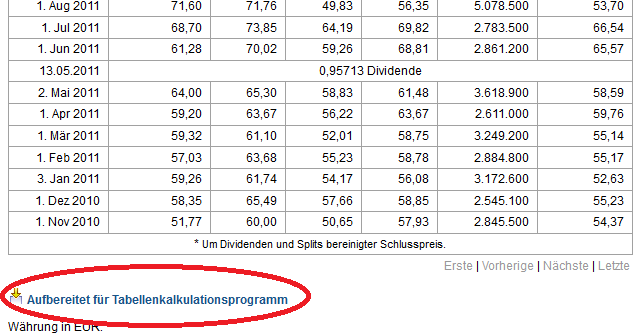 Am Ende der Auflistung können die Daten über „Aufbereitet für Tabellenkalkulationsprogramm“ exportiert werden. Damit speichern wir die Datei als BMW.csv.
Am Ende der Auflistung können die Daten über „Aufbereitet für Tabellenkalkulationsprogramm“ exportiert werden. Damit speichern wir die Datei als BMW.csv.
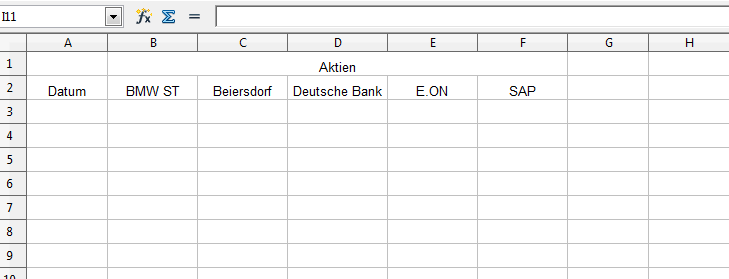
Zur Bearbeitung der Daten wird ein OpenOffice Calc-Datei namens Risiko_Rendite.ods erstellt. In Tabelle werden folgende Felder vorbereitet:
 Danach wird die Kursdatei BMW.csv mit der rechten Maustaste ausgewählt und geöffnet mit OpenOffice Calc.
Danach wird die Kursdatei BMW.csv mit der rechten Maustaste ausgewählt und geöffnet mit OpenOffice Calc.
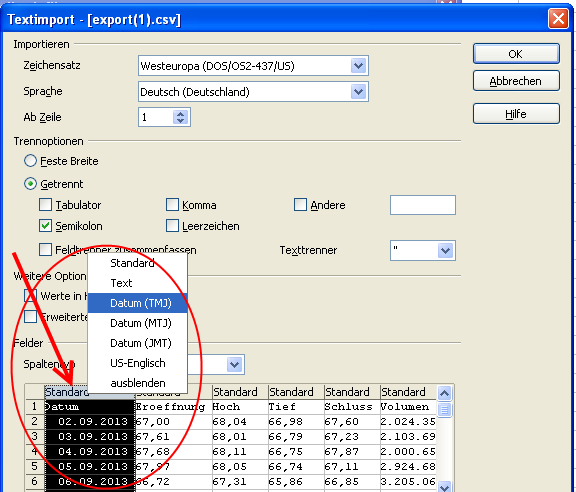
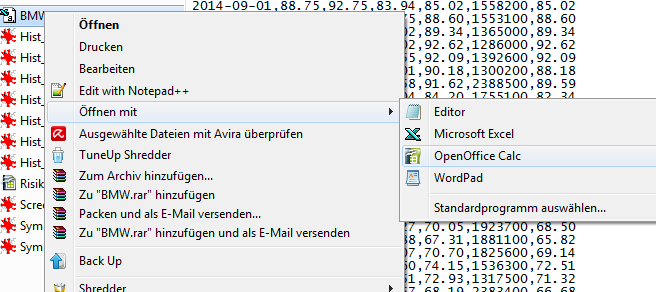 Die Textimport-Maske öffnet sich. Da Yahoo die Daten im US-amerikanischen Format bereitstellt, sind einige Einstellungen vorzunehmen:
Die Textimport-Maske öffnet sich. Da Yahoo die Daten im US-amerikanischen Format bereitstellt, sind einige Einstellungen vorzunehmen:
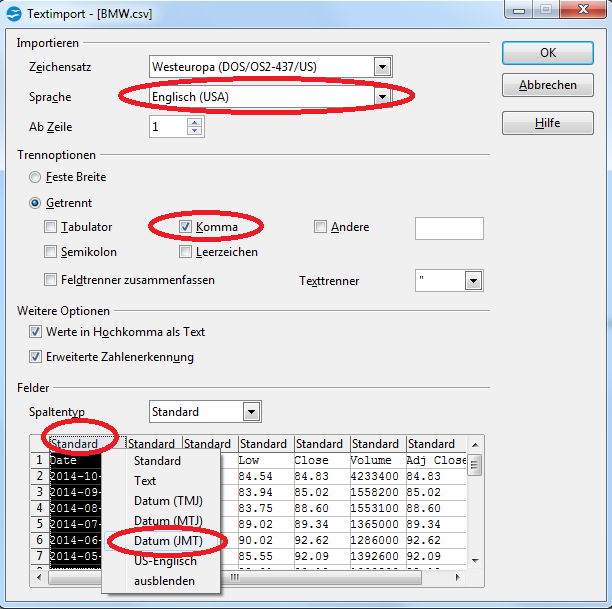 Zum einen ist die Sprache auf „Englisch (USA)“ einzustellen, damit der Dezimalpunkt in ein Dezimalkomma gewandelt wird. Desweiteren ist das Trennzeichen von „Semikolon“ auf „Komma“ umzustellen. Zuletzt muss die erste Spalte als Datum im Format „JMT“ (Jahr-Monat-Tag) definiert werden.
Zum einen ist die Sprache auf „Englisch (USA)“ einzustellen, damit der Dezimalpunkt in ein Dezimalkomma gewandelt wird. Desweiteren ist das Trennzeichen von „Semikolon“ auf „Komma“ umzustellen. Zuletzt muss die erste Spalte als Datum im Format „JMT“ (Jahr-Monat-Tag) definiert werden.
Mit dem „OK“-Button wird das OpenOffice-Dokument geöffnet, das in den ersten Zeilen wie folgt aussehen sollte:
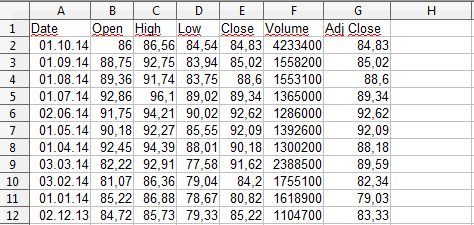 Insgesamt werden 7 Spalten ausgegeben. Das Datum (Date), der Eröffnungskurs (Open), der Höchstkurs (High), der Tiefstkurs (Low), der Schlusskurs (Close), das Handelsvolumen (Volume) und der „bereinigte“ Schlusskurs (Adjusted Close).
Insgesamt werden 7 Spalten ausgegeben. Das Datum (Date), der Eröffnungskurs (Open), der Höchstkurs (High), der Tiefstkurs (Low), der Schlusskurs (Close), das Handelsvolumen (Volume) und der „bereinigte“ Schlusskurs (Adjusted Close).
Letzterer berücksichtigt Dividenden und Aktiensplits. Dabei entsprechen die aktuellen Kurse den tatsächlichen Kursen, während die Kurse vor Dividenden oder Splits angepaßt werden.
Nun markieren wir die Zellen A2 bis A49, kopieren sie und fügen sie in unsere Arbeitsdatei Risiko_Rendite.ods ab Zelle A3 ein (Zelle A3 markieren und mit rechter Maustaste einfügen). Mit dem „bereinigten Schlusskurs verfahren wir identisch, d.h. wir markieren die Zellen G2 bis G49 und fügen sie ab Zeile B3 ein.
Das Ergebnis sieht wie folgt aus:
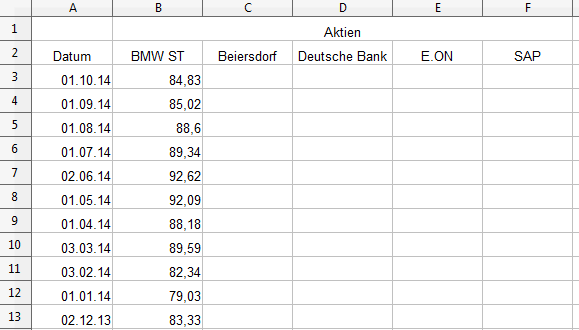 Auf die gleiche Weise gehen wir nun für die Kursdaten von Beiersdorf (Symbol: BEI.DE), der Deutschen Bank (DBK.DE), E.ON (EOAN.DE) und SAP (SAP.DE) vor. Allerdings reicht es nun aus, die „bereinigten“ Schlusskurse der einzelnen Titel zu kopieren und in unsere Arbeitsdatei einzufügen, da wir die Datumsfelder (welche ja für alle Werte gleich sind) bereits aus der BMW.csv heraus integriert haben.
Auf die gleiche Weise gehen wir nun für die Kursdaten von Beiersdorf (Symbol: BEI.DE), der Deutschen Bank (DBK.DE), E.ON (EOAN.DE) und SAP (SAP.DE) vor. Allerdings reicht es nun aus, die „bereinigten“ Schlusskurse der einzelnen Titel zu kopieren und in unsere Arbeitsdatei einzufügen, da wir die Datumsfelder (welche ja für alle Werte gleich sind) bereits aus der BMW.csv heraus integriert haben.
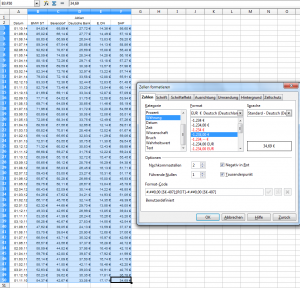
Nun wollen wir die Daten noch etwas freundlicher darstellen. Dazu markieren wir alle Kursfelder, wählen mit der rechten Maustaste „Zellen formatieren“ und selektieren „Währung“.
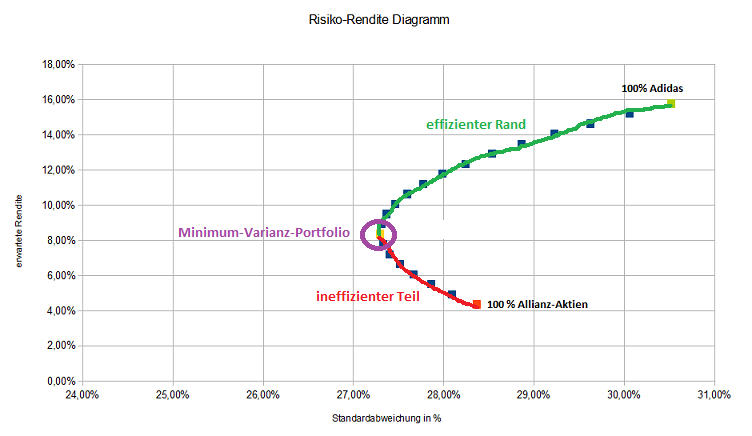
Hinweis: Durch Anklicken kann die nebenstehende Grafik vergrößert werden (mit dem „Zurück“-Button des Browers kann zum Artikel zurückgekehrt werden).
Berechnung der monatlichen Renditen
Die Formel für die Rendite einer Periode lautet:
Wobei Pt der aktuelle Kurs und Pt-1 der Kurs der Vorperiode ist. Dt ist die Dividende in der aktuellen Periode.
Beispiel: Der aktuelle Kurs beträgt 105 €, der Kurs vor einem Monat betrug 100 € und im laufenden Monat wurde ein Dividende von 5 € ausgeschüttet:
oder
Da wir mit „bereinigten“ Kursen arbeiten, sind Dividenden bereits in den Zahlen verarbeitet. Somit läßt sich die Berechnung vereinfachen.
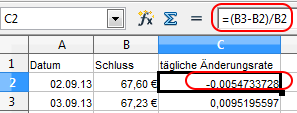
 Statt „=(B3-B4)/B4“ kann gleichwertig „=B3/B4-1“ verwendet werden.
Statt „=(B3-B4)/B4“ kann gleichwertig „=B3/B4-1“ verwendet werden.
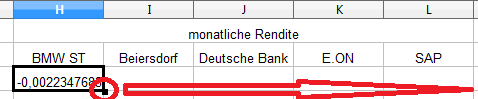 Die Berechnungen müssen nun nicht per Hand für alle Werte eingetragen werden. Wir markieren die Zelle H3 und gehen mit der Maus auf das kleine, schwarze Quadrat an der rechten, unteren Ecke. Der Mauszeiger verwandelt sich in ein „+“. Jetzt ziehen wir die Maus mit gedrückter, linker Maustaste bis zur Zelle L3.
Die Berechnungen müssen nun nicht per Hand für alle Werte eingetragen werden. Wir markieren die Zelle H3 und gehen mit der Maus auf das kleine, schwarze Quadrat an der rechten, unteren Ecke. Der Mauszeiger verwandelt sich in ein „+“. Jetzt ziehen wir die Maus mit gedrückter, linker Maustaste bis zur Zelle L3.
Die Berechnungen werden damit für die anderen Zellen übernommen.
 Zur Vervollständigung der restlichen Berechnungen markieren wir die Zellen H3 bis L3, ziehen die Maus auf das schwarze Quadrat der Zelle L3 und ziehen die Maus mit gedrückter, linker Maustaste nach unten bis zur Zeile 49 (zum ältesten Kurs in Zeile 50 gibt es kein Vorgänger-Kurs, so dass auch keine Rendite berechnet werden kann).
Zur Vervollständigung der restlichen Berechnungen markieren wir die Zellen H3 bis L3, ziehen die Maus auf das schwarze Quadrat der Zelle L3 und ziehen die Maus mit gedrückter, linker Maustaste nach unten bis zur Zeile 49 (zum ältesten Kurs in Zeile 50 gibt es kein Vorgänger-Kurs, so dass auch keine Rendite berechnet werden kann).
Wir lassen die Zellen markiert und wählen mit der rechten Maustaste „Zellen formatieren“.
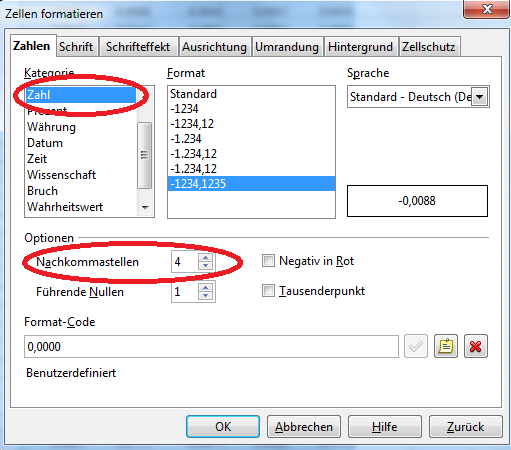 Nun reduzieren wir die Zahl der Nachkommastellen auf „4“, um die Übersichtlichkeit zu erhöhen.
Nun reduzieren wir die Zahl der Nachkommastellen auf „4“, um die Übersichtlichkeit zu erhöhen.
Das Resultat sieht wie folgt aus (zum Vergrößern bitte wieder auf die Grafik klicken):
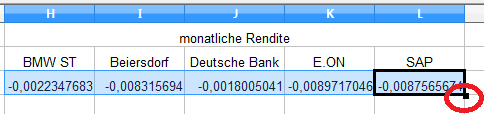
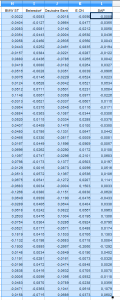 Der erste Wert bei BMW mit -0,0022 sagt aus, dass der Kurs im Vergleich zur Vorperiode um 0,22% gefallen ist.
Der erste Wert bei BMW mit -0,0022 sagt aus, dass der Kurs im Vergleich zur Vorperiode um 0,22% gefallen ist.
Berechnung der Rendite, Varianz und Standardabweichung
Die Berechnungen führen wir unterhalb der monatlichen Renditen durch. Doch zuvor wollen wir die Bezeichnungen festlegen, um uns später wieder zurechtzufinden.
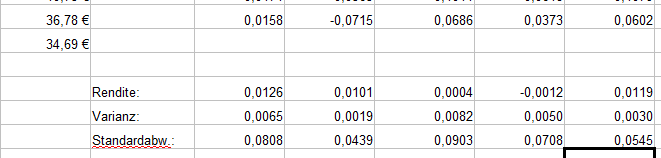
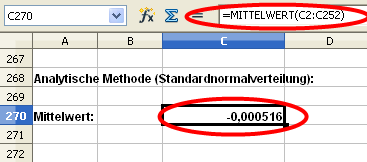
Danach berechnen wir die erwartete Rendite der BMW-Aktie. Diese entspricht dem Mittelwert der einzelnen Monatsrenditen:
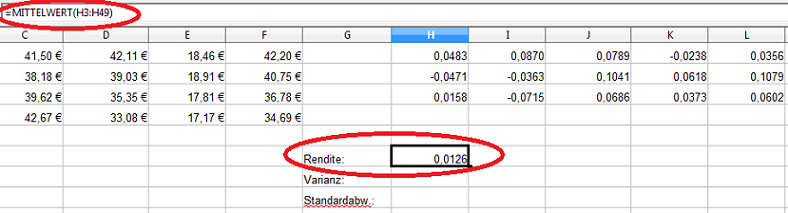 Die erwartete Rendite von BMW über den gesamten Zeitraum wird mit der Funktion „Mittelwert“ berechnet. Entweder tragen Sie in die Zelle die komplette Formel „=MITTELWERT(H3:H49)“ ein oder Sie tragen „=MITTELWERT(“ ein, markieren die betreffenden Zellen und bestätigen mit „ENTER“.
Die erwartete Rendite von BMW über den gesamten Zeitraum wird mit der Funktion „Mittelwert“ berechnet. Entweder tragen Sie in die Zelle die komplette Formel „=MITTELWERT(H3:H49)“ ein oder Sie tragen „=MITTELWERT(“ ein, markieren die betreffenden Zellen und bestätigen mit „ENTER“.
Danach klicken Sie einfach wieder in das kleine, schwarze Quadrat der Zelle H52 und ziehen die Maus bis zur Zelle L52, um die Renditen der weiteren Aktien auszugeben.
 Die Varianz berechnen wir auf die gleiche Art und Weise. Nur statt der Funktion „MITTELWERT“ verwenden wir die Funktion „VARIANZ“. Also Zelle H53 markieren und „=VARIANZ(H3:H49)“ (oder per Markierung der Zellen) einfügen. Anschließend übertragen Sie die Formeln wieder auf die Zellen I53 bis L53 wie zuvor beschrieben.
Die Varianz berechnen wir auf die gleiche Art und Weise. Nur statt der Funktion „MITTELWERT“ verwenden wir die Funktion „VARIANZ“. Also Zelle H53 markieren und „=VARIANZ(H3:H49)“ (oder per Markierung der Zellen) einfügen. Anschließend übertragen Sie die Formeln wieder auf die Zellen I53 bis L53 wie zuvor beschrieben.
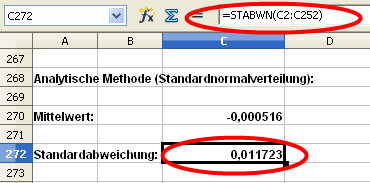
Die Standardabweichung ist die Wurzel der Varianz. Also tragen wir in die Zelle H54 „=WURZEL(H53)“ ein und übernehmen die Formel für die weiteren Zellen.
Berechnung der Korrelation
Zu Beginn stellen wir die fünf Aktien gegenüber, für die wir die Korrelation ausgeben wollen:
 Zur Berechnung der Korrelation stellt uns OpenOffice Calc die Funktion „Korrel()“ zur Verfügung.
Zur Berechnung der Korrelation stellt uns OpenOffice Calc die Funktion „Korrel()“ zur Verfügung.
Einzugeben sind zwei Datenbereiche in der Form (Daten_1;Daten_2).
Um die Korrelation zwischen BMW und BMW zu ermitteln, gehen wir auf die Zelle H57 und geben „=KORREL(“ ein.Nun werden die Zellen H3 bis H49 ausgewählt und ein Semikolon eingegeben. Anschließend werden nochmals die Zellen H3 bis H49 ausgewählt, da wir ja die Korrelation für BMW mit BMW ausgeben, und mit „ENTER“ übernommen. Selbstverständlich können Sie auch direkt die Datenbereiche eingeben.
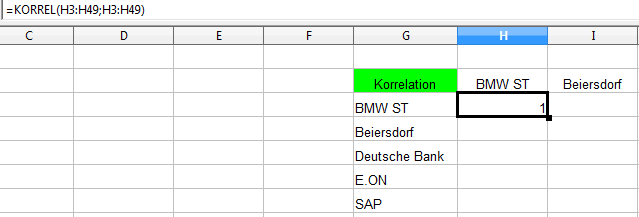 Unabhängig welchen Weg Sie gehen, lautet die Funktion der Zelle „=KORREL(H3:H49;H3:H49)“.
Unabhängig welchen Weg Sie gehen, lautet die Funktion der Zelle „=KORREL(H3:H49;H3:H49)“.
Analog können wir für die weiteren Korrelation der ersten Zeile vorgehen. Für die Zelle I57 (BMW – Beiersdorf) muss die Funktion „=KORREL(H3:H49;I3:I49)“ eingegeben werden, für J57 (BMW – Deutsche Bank) entsprechend „=KORREL(H3:H49;J3:J49)“ usw.
In der zweiten Zeile beginnen wir mit der Paarung Beiersdorf – Beiersdorf, da die Korrelation Beiersdorf zu BMW bereits zuvor berechnet wurde. Der Datenbereich von Beiersdorf ist bekanntlich I3 bis I49, folglich lautet die Funktion „=KORREL(I3:I49;J3:J49)“.
Wie die Funktionen im einzelnen aussehen, zeigt die folgende Grafik.
 Möglicherweise ist Ihnen aufgefallen, dass im Datenbereich teilweise ein „$“ eingesetzt wurde. Das „$“-Zeichen definiert die darauffolgende Zeile oder Spalte als Konstante. Durch den Einsatz der Konstanten können wir uns Tipparbeit sparen.
Möglicherweise ist Ihnen aufgefallen, dass im Datenbereich teilweise ein „$“ eingesetzt wurde. Das „$“-Zeichen definiert die darauffolgende Zeile oder Spalte als Konstante. Durch den Einsatz der Konstanten können wir uns Tipparbeit sparen.
Wir haben zuvor bei den Renditen auf das kleine, schwarze Quadrat der Zelle H3 geklickt und die Maus mit gedrückter, linker Taste zum Feld L3 gezogen. Dadurch wurde aus „=(B3-B4)/B4“ in der Formel H3 in der Spalte J „(C3-C4)/C4″. Wäre die Funktion in H3 definiert mit „=($B3-$B4)/$B4“, so würde auch in den anderen Spalten „=($B3-$B4)/$B4“ stehen. Auf den gleichen Ablauf treffen wir in vertikaler Richtung. Nur das sich hier die Zeilennummern ändern, oder eben nicht, wenn wir das „$“-Symbol davorsetzen.
Zurück zu unserer Tabelle. Indem wir bei der Korrelationsberechnung zwischen BMW und BMW im Datenbereich 1 die Spalten als konstant festlegen „($H3:$H49;..“ bleibt der erste Bereich beim Kopieren nach rechts (denn nichts anderes als Kopieren ist es, wenn wir über das schwarze Quadrat eine Funktion auf andere Zellen übertragen) im auf Spalte H, also BMW bezogen. Der zweite Datenbereich dagegen ist ohne Dollarzeichen und entsprechend variabel, so dass der Bereich erst auf Beiersdorf, dann auf die Deutsche Bank, E.ON und SAP zeigt.
Unabhängig wie Sie persönlich vorgehen, das Ergebnis sollte wie folgt aussehen:
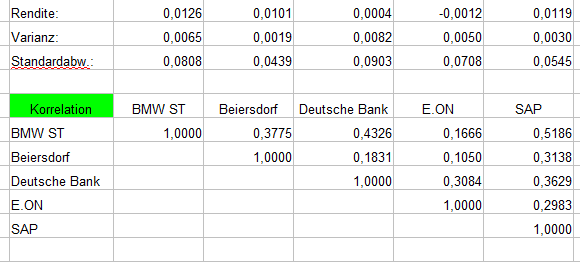 Aus der Tabelle können wir neben den einzelnen Korrelationen verschiedene Informationen auslesen:
Aus der Tabelle können wir neben den einzelnen Korrelationen verschiedene Informationen auslesen:
- Die Korrelation zwischen zwei gleichen Aktien muss immer 1 sein (vollständig positive Korrelation).
- Es liegen keine negativen Korrelationen vor.
- Es liegen keine hohen Korrelationen (> 0,7) vor. Hätten wir Aktien aus gleichen Sektoren verwendet, wäre die Korrelation im Schnitt sicherlich deutlich höher.
- Die kleinste Korrelation liegt zwischen Beierdorf und E.ON (0,1050) vor, was einer sehr kleinen Korrelation entspricht (klein entspricht üblicherweise < 0,3).